题目内容
11.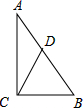 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,那么下列结论错误的是( )
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,那么下列结论错误的是( )| A. | ∠A+∠DCB=90° | B. | ∠ADC=2∠B | C. | AB=2CD | D. | BC=CD |
分析 根据直角三角形斜边上的中线性质得出CD=AD=BD,根据等边对等角得出∠DCB=∠B,再逐个判断即可.
解答 解:A、∵在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD=BD=$\frac{1}{2}$AB,
∴∠DCB=∠B,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠A+∠DCB=90°,故本选项错误;
B、∵∠DCB=∠B,∠ADC=∠B+∠DCB,
∴∠ADC=2∠B,故本选项错误;
C、∵在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,
∴AB=2CD,故本选项错误;
D、根据已知不能推出BC=CD,故本选项正确;
故选D.
点评 本题考查了直角三角形斜边上的中线性质,等腰三角形性质的应用,能熟记直角三角形斜边上的中线等于斜边的一半是解此题的关键.

练习册系列答案
相关题目
20.下列计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{2}$=2 | B. | $\sqrt{3}$-$\sqrt{3}$=0 | C. | $\sqrt{2}$×$\sqrt{2}$=4 | D. | $\sqrt{(-3)^{2}}$=-3 |
6.某公路的干线上有相距108公里的A、B两个车站,某日16点整,甲、乙两车分别从A、B两站同时出发,相向而行,已知甲车的速度为45公里/时,乙车的速度为36公里/时,则两车相遇的时间是( )
| A. | 16时20分 | B. | 17时20分 | C. | 17时40分 | D. | 16时40分 |
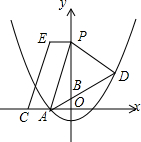 在平面直角坐标系中,A(-2,0),B(0,1),C(-4,0).点D(4,m)在直线AB上,抛物线y=$\frac{1}{4}$x2+bx+c恰好过A、D两点,点P(0,n)是抛物线对称轴上的一动点,将点P向左平移2个单位长度,对应点为E,连接PF、CE.
在平面直角坐标系中,A(-2,0),B(0,1),C(-4,0).点D(4,m)在直线AB上,抛物线y=$\frac{1}{4}$x2+bx+c恰好过A、D两点,点P(0,n)是抛物线对称轴上的一动点,将点P向左平移2个单位长度,对应点为E,连接PF、CE.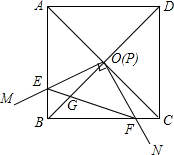 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1),(2),(3),(5).
如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1),(2),(3),(5).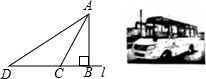 如图是我市投入使用的“大鼻子”校车,其安全隐患主要是超速和超载,某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验,先在笔直的车道l旁边选取一点A,再在l上确定点B,使AB⊥l,测得AB的长为30米,又在l上选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.
如图是我市投入使用的“大鼻子”校车,其安全隐患主要是超速和超载,某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验,先在笔直的车道l旁边选取一点A,再在l上确定点B,使AB⊥l,测得AB的长为30米,又在l上选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.