题目内容
6．某公路的干线上有相距108公里的A、B两个车站，某日16点整，甲、乙两车分别从A、B两站同时出发，相向而行，已知甲车的速度为45公里/时，乙车的速度为36公里/时，则两车相遇的时间是（ ）| A． | 16时20分 | B． | 17时20分 | C． | 17时40分 | D． | 16时40分 |
分析 在相遇问题中，常用的相等关系为：两车所走的路程和=两个站之间的总路程，即S甲+S乙=SAB．先利用相等关系求出相遇所用的时间，再换算成时间即可．
解答 解：设两车相遇需要x小时，根据题意，
得：45x+36x=108，
解得：x=1$\frac{1}{3}$，
所以两车相遇的时间是16+1$\frac{1}{3}$=17$\frac{1}{3}$，即17点20分，
故选：B．
点评 本题考查一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的数量关系，列出方程，再求解．此题要熟悉行程问题中的相遇问题的相等关系，并能熟练运用．相遇问题中，常用的相等关系为：两车所走的路程和=两个站之间的总路程．
练习册系列答案
相关题目
11．
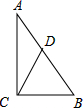如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，那么下列结论错误的是（ ）
如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，那么下列结论错误的是（ ）| A． | ∠A+∠DCB=90° | B． | ∠ADC=2∠B | C． | AB=2CD | D． | BC=CD |
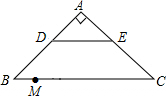如图，在Rt△ABC中，∠A=90°，AB=AC，BC=20，DE是△ABC的中位线，点M是边BC上一点，BM=3，点N是线段MC上的一个动点，连接DN，ME，DN与ME相交于点O．若△OMN是直角三角形，则DO的长是$\frac{25}{6}$或$\frac{50}{13}$．
如图，小明想通过测量知道一建筑物AB的高度．他通过测量获得了以下的数据：站在点C处测得建筑物顶端A的仰角为48°，他的眼睛距离地面的高度CD=1.6m，C，B间的距离为12m．请你根据测量获得的数据，计算出建筑物AB的高度是多少？
1．若x2-x-1=0，则$\frac{{{x^4}+2x+1}}{x^5}$的值是（ ）
| A． | 1 | B． | 2 | C． | -1 | D． | 0 |
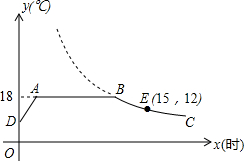我市某花卉生产基地在气温较低时，用装有恒温系统的温室栽培一种在自然光照且温度为18℃的条件下生长最快的新品种，如图是某天恒温系统从开启到关闭及关闭后，温室内温度y（℃）随时间x（小时）变化的函数图象，其中DA段所满足的表达式为y=5x+13，BC段是反比例函数图象的一部分，点E是BC段上一点．请根据图中信息解答下列问题：
15．如（x2+mx+1）（x3-3x+1）乘积中不含x4项，则m的值为（ ）
| A． | -3 | B． | 3 | C． | 0 | D． | 1 |