题目内容
16.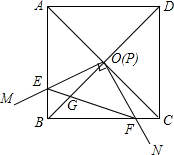 如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1),(2),(3),(5).
如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是(1),(2),(3),(5).(1)EF=$\sqrt{2}$OE;(2)S四边形OEBF:S正方形ABCD=1:4;(3)BE+BF=$\sqrt{2}$OA;(4)在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;(5)OG•BD=AE2+CF2.
分析 (1)由四边形ABCD是正方形,直角∠MPN,易证得△BOE≌△COF(ASA),则可证得结论;
(2)由(1)易证得S四边形OEBF=S△BOC=$\frac{1}{4}$S正方形ABCD,则可证得结论;
(3)由BE=CF,可得BE+BF=BC,然后由等腰直角三角形的性质,证得BE+BF=$\sqrt{2}$OA;
(4)首先设AE=x,则BE=CF=1-x,BF=x,继而表示出△BEF与△COF的面积之和,然后利用二次函数的最值问题,求得答案;
(5)易证得△OEG∽△OBE,然后由相似三角形的对应边成比例,证得OG•OB=OE2,再利用OB与BD的关系,OE与EF的关系,即可证得结论.
解答 解:(1)∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∴∠BOF+∠COF=90°,
∵∠EOF=90°,
∴∠BOF+∠COE=90°,
∴∠BOE=∠COF,
在△BOE和△COF中,
$\left\{\begin{array}{l}{∠BOE=∠COF}\\{OB=OC}\\{∠OBE=∠OCF}\end{array}\right.$,
∴△BOE≌△COF(ASA),
∴OE=OF,BE=CF,
∴EF=$\sqrt{2}$OE;故正确;
(2)∵S四边形OEBF=S△BOE+S△BOE=S△BOE+S△COF=S△BOC=$\frac{1}{4}$S正方形ABCD,
∴S四边形OEBF:S正方形ABCD=1:4;故正确;
(3)∴BE+BF=BF+CF=BC=$\sqrt{2}$OA;故正确;
(4)过点O作OH⊥BC,
∵BC=1,
∴OH=$\frac{1}{2}$BC=$\frac{1}{2}$,
设AE=x,则BE=CF=1-x,BF=x,
∴S△BEF+S△COF=$\frac{1}{2}$BE•BF+$\frac{1}{2}$CF•OH=$\frac{1}{2}$x(1-x)+$\frac{1}{2}$(1-x)×$\frac{1}{2}$=-$\frac{1}{2}$(x-$\frac{1}{4}$)2+$\frac{9}{32}$,
∵a=-$\frac{1}{2}$<0,
∴当x=$\frac{1}{4}$时,S△BEF+S△COF最大;
即在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{1}{4}$;故错误;
(5)∵∠EOG=∠BOE,∠OEG=∠OBE=45°,
∴△OEG∽△OBE,
∴OE:OB=OG:OE,
∴OG•OB=OE2,
∵OB=$\frac{1}{2}$BD,OE=$\frac{\sqrt{2}}{2}$EF,
∴OG•BD=EF2,
∵在△BEF中,EF2=BE2+BF2,
∴EF2=AE2+CF2,
∴OG•BD=AE2+CF2.故正确.
故答案为:(1),(2),(3),(5).
点评 此题属于四边形的综合题.考查了正方形的性质,旋转的性质、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理以及二次函数的最值问题.注意掌握转化思想的应用是解此题的关键.

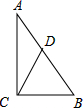 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,那么下列结论错误的是( )
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,那么下列结论错误的是( )| A. | ∠A+∠DCB=90° | B. | ∠ADC=2∠B | C. | AB=2CD | D. | BC=CD |
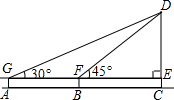 某校数学兴趣小组的同学用学到的解直角三角形的知识,测量聊城摩天轮圆心D到地面AC的高度CD,如图,在空地的A处,他们利用测角仪器测得CD顶端的仰角为30°,沿AC方向前进40米到达B处,又测得CD顶端的仰角为45°,已知测交仪器的高度为1.2米,求摩天轮圆心到地面的高度.($\sqrt{3}$≈1.732,精确到0.1米)
某校数学兴趣小组的同学用学到的解直角三角形的知识,测量聊城摩天轮圆心D到地面AC的高度CD,如图,在空地的A处,他们利用测角仪器测得CD顶端的仰角为30°,沿AC方向前进40米到达B处,又测得CD顶端的仰角为45°,已知测交仪器的高度为1.2米,求摩天轮圆心到地面的高度.($\sqrt{3}$≈1.732,精确到0.1米)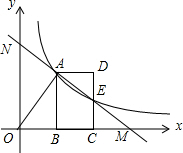 如图,O为原点,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).
如图,O为原点,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).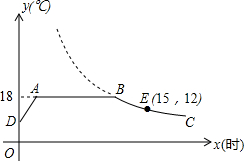 我市某花卉生产基地在气温较低时,用装有恒温系统的温室栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,温室内温度y(℃)随时间x(小时)变化的函数图象,其中DA段所满足的表达式为y=5x+13,BC段是反比例函数图象的一部分,点E是BC段上一点.请根据图中信息解答下列问题:
我市某花卉生产基地在气温较低时,用装有恒温系统的温室栽培一种在自然光照且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,温室内温度y(℃)随时间x(小时)变化的函数图象,其中DA段所满足的表达式为y=5x+13,BC段是反比例函数图象的一部分,点E是BC段上一点.请根据图中信息解答下列问题: