题目内容
8.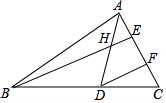 如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.求∠FDC和∠AHB的度数.
分析 由∠AHB=∠DAC+∠BEA,只要求出∠DAC即可解决问题.
解答 解:∵BE⊥AC,
∴∠BEC=90°,
∵DF∥BE ,
,
∴∠BEC=∠DFC=90°,
∵∠C=64°,
∴∠FDC=180°-(∠DFC+∠C)
=180°-(90°+64°)
=26°,
∵∠ABC=36°,∠C=64°,
∴∠BAC=180°-∠ABC-∠C=180°-36°-64°=80°,
∵AD平分∠BAC,
∴∠DAC=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×80°=40°,
∴∠AHB=∠DAC+∠BEA
=40°+90°
=130°.
点评 本题考查三角形内角和定理、三角形的外角的性质、平行线的性质、垂线的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
3.若a<b,则下列各式错误的是( )
| A. | a-3<b-3 | B. | -2a<-2b | C. | 0.7a<0.7b | D. | -$\frac{a}{4}$$>-\frac{b}{4}$ |
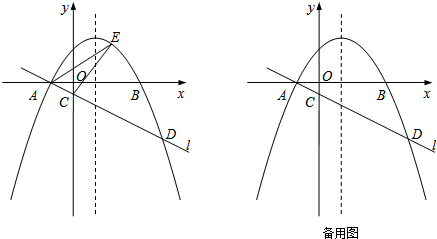
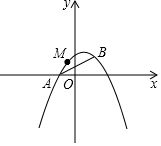 如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.
如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.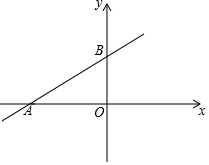 如图,在平面直角坐标系中,一次函数y=kx+6的图象分别与x轴,y轴交于点A,B,点A的坐标为(-8,0).
如图,在平面直角坐标系中,一次函数y=kx+6的图象分别与x轴,y轴交于点A,B,点A的坐标为(-8,0).