题目内容
16.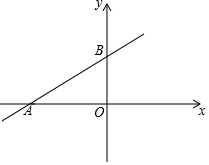 如图,在平面直角坐标系中,一次函数y=kx+6的图象分别与x轴,y轴交于点A,B,点A的坐标为(-8,0).
如图,在平面直角坐标系中,一次函数y=kx+6的图象分别与x轴,y轴交于点A,B,点A的坐标为(-8,0).(1)点B的坐标为(0,6);
(2)在第二象限内是否存在点P,使得以P、O、A为顶点的三角形与△OAB相似?若存在,请求出所有符台条件的点P的坐标:若不存在,请说明理由.
分析 (1)令x=0可得y=6,由此可知B(0,6);
(2)如图,以OA、OB为边作矩形OAP3B,连接OP3,作OP1⊥AB于P1,作AP2⊥OP3于P2.易证△OAP1,△OAP2,△OAP3均与△AOB相似,易知P3(-8,6).构建一次函数求出交点P1、P2的坐标,再由当△OAP4∽△BOA时,可得$\frac{OA}{OB}$=$\frac{O{P}_{4}}{OA}$,推出OP4=$\frac{32}{3}$,由此可得P4的坐标;
解答 解:(1)令x=0,得到y=6,
∴B(0,6).
故答案为(0,6).
(2)如图,以OA、OB为边作矩形OAP3B,连接OP3,作OP1⊥AB于P1,作AP2⊥OP3于P2.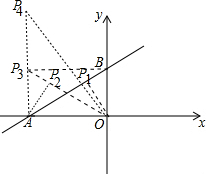
易证△OAP1,△OAP2,△OAP3均与△AOB相似,易知P3(-8,6).
∵直线AB的解析式为y=$\frac{3}{4}$x+6,
∴直线OP1的解析式为y=-$\frac{4}{3}$x,
由$\left\{\begin{array}{l}{y=\frac{3}{4}x+6}\\{y=-\frac{4}{3}x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{72}{25}}\\{y=\frac{96}{25}}\end{array}\right.$,
∴P1(-$\frac{72}{25}$,$\frac{96}{25}$),
∵直线OP3的解析式为y=-$\frac{3}{4}$x,
∴直线OP2的解析式为y=$\frac{4}{3}$x+$\frac{32}{3}$,
由$\left\{\begin{array}{l}{y=-\frac{3}{4}x}\\{y=\frac{4}{3}x+\frac{32}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{128}{25}}\\{y=\frac{96}{25}}\end{array}\right.$,
∴P2(-$\frac{128}{25}$,$\frac{96}{25}$),
当△OAP4∽△BOA时,
可得$\frac{OA}{OB}$=$\frac{O{P}_{4}}{OA}$,
∴OP4=$\frac{32}{3}$,
∴P4(-8,$\frac{32}{3}$),
综上所述,满足条件的点P的坐标为P1(-$\frac{72}{25}$,$\frac{96}{25}$),P2(-$\frac{128}{25}$,$\frac{96}{25}$),P3(-8,6),P4(-8,$\frac{32}{3}$).
点评 此题考查了一次函数综合题相似三角形的性质,坐标与图形性质,利用了分类讨论及数形结合的思想,解题的关键学会构建一次函数,利用方程组确定两个函数图象的交点坐标,属于中考常考题型.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. | 3×108 | B. | 0.3×108 | C. | 3×109 | D. | 0.3×109 |
| A. | 3cm,8cm,12cm | B. | 3cm,4cm,5cm | ||
| C. | 6cm,9cm,15cm | D. | 100cm,200cm,300cm |
 如图,已知AB∥CD,∠1=60°,则∠2=( )
如图,已知AB∥CD,∠1=60°,则∠2=( )| A. | 90° | B. | 120° | C. | 60° | D. | 15° |
 如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )
如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )| A. | x=3 | B. | x=-3 | C. | x=4 | D. | x=-4 |
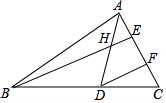 如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.