题目内容
17.计算:(1)$\frac{1}{x-3}$-$\frac{1}{3+x}$
(2)m-1+$\frac{2m-6}{{m}^{2}-9}$÷$\frac{2m+2}{m+3}$.
分析 根据分式的运算法则即可求出答案.
解答 解:(1)原式=$\frac{x+3}{(x-3)(x+3)}$-$\frac{(x-3)}{(x+3)(x-3)}$
=$\frac{6}{(x-3)(x+3)}$
(2)原式=m-1+$\frac{2(m-3)}{(m-3)(m+3)}$×$\frac{m+3}{2(m+1)}$
=m-1+$\frac{1}{m+1}$
=$\frac{{m}^{2}-1}{m+1}$-$\frac{1}{m+1}$
=$\frac{{m}^{2}}{m+1}$
点评 本题考查分式的运算法则,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
相关题目
2.已知点(-2,a),(3,b)都在直线y=2x+m上,对于a,b的大小关系叙述正确的是( )
| A. | a>b | B. | a<b | C. | a≥b | D. | a≤b |
6.贵州省3月份发布了2017年大数据十大工程,其中拟定了贵阳大数据交易所年度发展目标:交易会员达到2000家,交易规模累计300000000元人民币以上,将300000000这个数用科学记数法可表示为( )
| A. | 3×108 | B. | 0.3×108 | C. | 3×109 | D. | 0.3×109 |
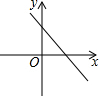
4. 如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )
如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )
 如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )
如图,直线y=kx+b过点A(0,3)和点B(-4,0),则方程kx+b=0的解是( )| A. | x=3 | B. | x=-3 | C. | x=4 | D. | x=-4 |

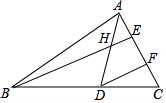 如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE.
如图,在△ABC中,∠ABC=36°,∠C=64°,AD平分∠BAC,交BC于D,BE⊥AC,交AD、AC于H、E,且DF∥BE. “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了乌龟所行的路程y1与出发所行的时间x的关系.
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场,图中的函数图象刻画了乌龟所行的路程y1与出发所行的时间x的关系. 已知一次函数y=kx+b的图象经过点A(2,0),与y轴交于点B(0,4).
已知一次函数y=kx+b的图象经过点A(2,0),与y轴交于点B(0,4).