题目内容
20.解方程组{$\left\{\begin{array}{l}{\frac{4}{x}+\frac{3}{y}=10}\\{\frac{9}{x}-\frac{7}{y}=-5}\end{array}\right.$,设$α=\frac{1}{x}$,$β=\frac{1}{y}$,先把原方程化为整式方程,然后再求出原方程组的解.分析 根据方程特点设$α=\frac{1}{x}$,$β=\frac{1}{y}$,则原方程可化为关于α、β的整式方程组,解方程组即可求解.
解答 解:设$α=\frac{1}{x}$,$β=\frac{1}{y}$,则
$\left\{\begin{array}{l}{4α+3β=10}\\{9α-7β=-5}\end{array}\right.$,
解得$\left\{\begin{array}{l}{α=1}\\{β=2}\end{array}\right.$,
则x=1,y=$\frac{1}{2}$,
经检验可知,$\left\{\begin{array}{l}{x=1}\\{y=\frac{1}{2}}\end{array}\right.$是原方程组的解.
故原方程组的解是$\left\{\begin{array}{l}{x=1}\\{y=\frac{1}{2}}\end{array}\right.$.
点评 本题考查用换元法解分式方程的能力,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.

练习册系列答案
相关题目

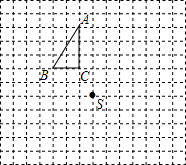 △ABC和点S都在正方形网格的格点上.
△ABC和点S都在正方形网格的格点上.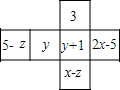 如图是一个正方体的平面展开图,如果正方体相对的两个面上的式子的值相等,求x,y,z的值.
如图是一个正方体的平面展开图,如果正方体相对的两个面上的式子的值相等,求x,y,z的值.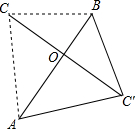 如图,△ABC的三边BC,AC,AB的长分别为3cm,4cm,5cm,把△ABC沿最长边AB翻折得到△ABC′的位置.
如图,△ABC的三边BC,AC,AB的长分别为3cm,4cm,5cm,把△ABC沿最长边AB翻折得到△ABC′的位置.


