题目内容
17.先化简,再求值:($\frac{a-1}{{a}^{2}-4a+4}$-$\frac{a+2}{{a}^{2}-2a}$)÷($\frac{4}{a}$-1),其中a是方程a2-4a+2=0的解.分析 原式括号中两项通分并利用同分母分式的加减法则计算,同时利用除法法则变形,约分得到最简结果,把已知等式变形后代入计算即可求出值.
解答 解:原式=[$\frac{a-1}{(a-2)^{2}}$-$\frac{a+2}{a(a-2)}$]÷$\frac{4-a}{a}$=$\frac{4-a}{a(a-2)^{2}}$•$\frac{a}{4-a}$=$\frac{1}{{a}^{2}-4a+4}$,
由a2-4a+2=0,得a2-4a=-2,
则原式=$\frac{1}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
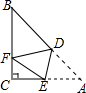 如图,在Rt△ABC中,已知∠C=90°,AC=6,将△ABC折叠,折痕是DE,折叠后点A恰好落在BC边上的点F处,若CE=2CF,则CF=6($\sqrt{5}$-2).
如图,在Rt△ABC中,已知∠C=90°,AC=6,将△ABC折叠,折痕是DE,折叠后点A恰好落在BC边上的点F处,若CE=2CF,则CF=6($\sqrt{5}$-2).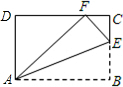 如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24cm,△ECF的周长为8cm,四边形纸片ABCD的周长为32cm.
如图,将四边形纸片ABCD沿AE向上折叠,使点B落在DC边上的点F处.若△AFD的周长为24cm,△ECF的周长为8cm,四边形纸片ABCD的周长为32cm.
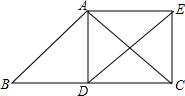 如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作?ABDE,连接AD,EC.求证:四边形ADCE是矩形.
如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作?ABDE,连接AD,EC.求证:四边形ADCE是矩形.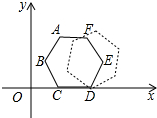 如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(47,2)的是点D.
如图的平面直角坐标系中有一个正六边形ABCDEF,其中C、D的坐标分别为(1,0)和(2,0).若在无滑动的情况下,将这个六边形沿着x轴向右滚动,则在滚动过程中,这个六边形的顶点A、B、C、D、E、F中,会过点(47,2)的是点D.