题目内容
12.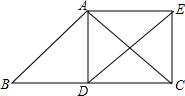 如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作?ABDE,连接AD,EC.求证:四边形ADCE是矩形.
如图,在△ABC中,AB=AC,D为BC边的中点,以AB、BD为邻边作?ABDE,连接AD,EC.求证:四边形ADCE是矩形.
分析 由等腰三角形的三线合一性质得出AD⊥BC,BD=CD,∠ADC=90°,由平行四边形的性质得出AE∥BD,AE=BD,得出AE∥CD,AE=CD,证出四边形ADCE是平行四边形,即可得出结论.
解答 证明:∵AB=AC,D为BC边的中点,
∴AD⊥BC,BD=CD,
∴∠ADC=90°,
∵四边形ABDE是平行四边形,
∴AE∥BD,AE=BD,
∴AE∥CD,AE=CD,
∴四边形ADCE是平行四边形,
又∵∠ADC=90°,
∴四边形ADCE是矩形.
点评 本题考查了等腰三角形的性质、平行四边形的判定与性质、矩形的判定;熟练掌握等腰三角形的性质和平行四边形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
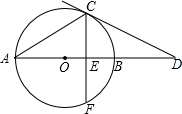 如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.
如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°.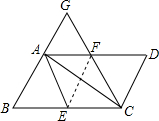 如图,将?ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,连接AE、CF,若四边形AEFG为菱形,则AD与AB的数量关系是AD=2AB.
如图,将?ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处,连接AE、CF,若四边形AEFG为菱形,则AD与AB的数量关系是AD=2AB.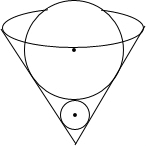 如图,在一个轴截面为等边三角形的圆锥形容器内放置两个密度相同的金属球,两球均与容器壁紧贴,且大球恰好压在小球上,则大球质量是小球的27倍.
如图,在一个轴截面为等边三角形的圆锥形容器内放置两个密度相同的金属球,两球均与容器壁紧贴,且大球恰好压在小球上,则大球质量是小球的27倍.