题目内容
2.在平行四边形ABCD中,AC与BD相交于点O,BD=2,将△ABC沿直线AC翻折,点B落在点B′处,如果B′O⊥BD,那么DB′的长为$\sqrt{2}$.分析 先根据题意画出图形,由平行四边形的性质可知OB=OD=1,然后由折叠的性质可知:OB=OB′=1,在Rt△DOB′中,由勾股定理可求得DB′=$\sqrt{2}$.
解答 解:如图所示:
∵四边形ABCD为平行四边形,
∴OB=OD=1.
由折叠的性质可知:OB=OB′=1.
∵B′O⊥BD,
∴△DOB′为直角三角形.
∴$DB′=\sqrt{D{O}^{2}+OB{′}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题主要考查的是翻折的性质、平行四边形的性质、勾股定理的应用,由平行四边形的性质和折叠的性质求得OD=OB′=1是解题的关键.

练习册系列答案
相关题目
12.计算(-3)+(-2)的结果是( )
| A. | -6 | B. | -5 | C. | 6 | D. | 5 |
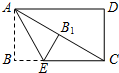 如图,在矩形ABCD中,AB=2cm,点E在BC上,且AE=EC.若将长方形沿AE折叠,点B恰好与AC上的点B1重合,则AE=$\frac{4\sqrt{3}}{3}$.
如图,在矩形ABCD中,AB=2cm,点E在BC上,且AE=EC.若将长方形沿AE折叠,点B恰好与AC上的点B1重合,则AE=$\frac{4\sqrt{3}}{3}$.