题目内容
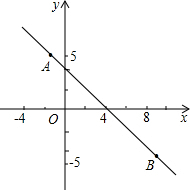 如图,已知直线y=kx+b过点(-1,5),且可由直线y=-x+2平移得到,
如图,已知直线y=kx+b过点(-1,5),且可由直线y=-x+2平移得到,(1)求直线y=kx+b的表达式;
(2)若B(m,5)在这条直线上,求m的值及该直线与y轴的交点.
考点:待定系数法求一次函数解析式,一次函数图象上点的坐标特征
专题:
分析:(1)根据两条直线平行的问题得到k=-1,再根据两条直线相交的问题把(-1,5)代入y=kx+b可求出b=4,于是可确定所求直线的解析式;
(2)再把B(m,5)代入y=kx+b,即可得出m的值,再令x=0即可得出答案.
(2)再把B(m,5)代入y=kx+b,即可得出m的值,再令x=0即可得出答案.
解答:解:(1)∵直线y=kx+b与直线y=-x+2平行,
∴k=-1,
把(-1,5)代入y=-x+b得b=4,
∴该直线的函数关系式为y=-x+4;
(2)把B(m,5)代入y=-x+4,可得出-m+4=5,
解得m=-1,
令x=0,得y=4,
∴该直线与y轴的交点(0,4).
∴k=-1,
把(-1,5)代入y=-x+b得b=4,
∴该直线的函数关系式为y=-x+4;
(2)把B(m,5)代入y=-x+4,可得出-m+4=5,
解得m=-1,
令x=0,得y=4,
∴该直线与y轴的交点(0,4).
点评:本题考查了两条直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.例如:若直线y1=k1x+b1与直线y2=k2x+b2平行,那么k1=k2.

练习册系列答案
相关题目
2013年12月15日,“玉兔号”月球车月面软着陆后离地球380000千米,能够看到地球等离子层的全貌.380000千米用科学记数法表示为( )
| A、38×107米 |
| B、3.8×108米 |
| C、3.8×109米 |
| D、0.38×109米 |
 如图,AB、CD是⊙O的直径,弦DE∥AB,连接AE、AC.求证:AE=AC.
如图,AB、CD是⊙O的直径,弦DE∥AB,连接AE、AC.求证:AE=AC.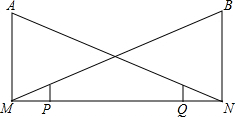 如图,王军同学上完晚自习放学步行回家,由路灯A走向路灯B,当他走到点P时,发现身后的影子顶部刚好接触到路灯A的底部M,当他向前再步行12m到达点Q时,发现身前他影子的顶部刚好接触到路灯B的底部N.已知王军的身高是1.6m,路灯A的高度AM是9.6m,且MP=NQ=x m.
如图,王军同学上完晚自习放学步行回家,由路灯A走向路灯B,当他走到点P时,发现身后的影子顶部刚好接触到路灯A的底部M,当他向前再步行12m到达点Q时,发现身前他影子的顶部刚好接触到路灯B的底部N.已知王军的身高是1.6m,路灯A的高度AM是9.6m,且MP=NQ=x m. (1)先观察下列等式,再完成题后问题:
(1)先观察下列等式,再完成题后问题: 如图,在一个长、宽分别为b,c的长方形铁片的四个角上各剪去一个边长为a的正方形(2a<c<b),然后按图中虚线折成一个长方形盒子(无盖),用代数式表示它的容积为
如图,在一个长、宽分别为b,c的长方形铁片的四个角上各剪去一个边长为a的正方形(2a<c<b),然后按图中虚线折成一个长方形盒子(无盖),用代数式表示它的容积为