题目内容
 如图,已知矩形ABCD,
如图,已知矩形ABCD,(1)请用尺规作图作∠B的角平分线交AD与点E,并画出△HMN,使它与△ABE相似,且相似比为1:2.(不写作法,保留作图痕迹)
(2)记△HMN的内切圆为S圆,求S圆:S△HMN.
考点:作图—相似变换,矩形的性质,三角形的内切圆与内心
专题:
分析:(1)直接作出∠B的平分线,进而得出作出AE和AB的垂直平分线分别交与点N,M,△HMN即为所求;
(2)首先得出△HMN是等腰直角三角形,再利用直角三角形内切圆半径公式r=
进而得出S圆和S△HMN,即可得出答案.
(2)首先得出△HMN是等腰直角三角形,再利用直角三角形内切圆半径公式r=
| a+b-c |
| 2 |
解答: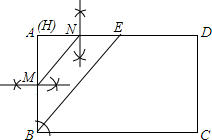 解:(1)作出∠B的角平线作出AE和AB的垂直平分线分别交与点N,M,△HMN即为所求;
解:(1)作出∠B的角平线作出AE和AB的垂直平分线分别交与点N,M,△HMN即为所求;
(2)∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴△ABE是等腰直角三角形,
∵△HMN与△ABE相似,
∴△HMN是等腰直角三角形,
设直角边为a,△HMN的内切圆:r=
a,
∴S圆=[
a]2π=
πa2,S△HMN=
a2,
∴S圆:S△HMN═(3-2
)π:1.
 解:(1)作出∠B的角平线作出AE和AB的垂直平分线分别交与点N,M,△HMN即为所求;
解:(1)作出∠B的角平线作出AE和AB的垂直平分线分别交与点N,M,△HMN即为所求;(2)∵AD∥BC,
∴∠AEB=∠EBC,
∵∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴△ABE是等腰直角三角形,
∵△HMN与△ABE相似,
∴△HMN是等腰直角三角形,
设直角边为a,△HMN的内切圆:r=
(2-
| ||
| 2 |
∴S圆=[
(2-
| ||
| 2 |
(3-2
| ||
| 2 |
| 1 |
| 2 |
∴S圆:S△HMN═(3-2
| 2 |
点评:此题主要考查了等腰直角三角形的性质以及相似三角形的判定与性质和直角三角形内切圆的性质,得出符合题意的三角形是解题关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
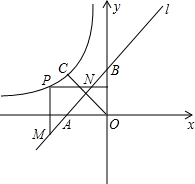 如图,直线l:y=x+2与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.反比例函数y=
如图,直线l:y=x+2与x轴、y轴分别交于A、B两点,点C与原点O关于直线l对称.反比例函数y=
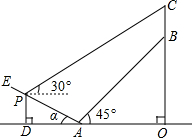 如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=
如图所示某人准备测量山顶铁塔BC的高度.在山的对面有一斜坡AE,斜坡的坡度为1:2(即tanα=