题目内容
11. 如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,
如图,A、B是双曲线y=$\frac{k}{x}$上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,(1)求四边形DCEB的面积.
(2)求k的值.
分析 (1)根据反比例函数k的几何意义得到三角形AOC与三角形BOE面积相等,进而得到四边形CDBE面积与三角形AOD面积相等,即可得到结果;
(2)根据D为OB中点,且三角形COD与三角形BOE相似,得到面积之比为1:4,求出三角形COD面积,得到三角形BOE面积,即可确定出k的值.
解答 解:(1)∵A、B是双曲线y=$\frac{k}{x}$上的两点,AC⊥x轴,BE⊥x轴,
∴S△AOC=S△BOE,即S△AOD+S△COD=S△COD+S四边形CDBE,
∵S△AOD=1,
∴S四边形CDBE=S△AOD=1;
(2)∵D为OB中点,△COD∽△EOB,
∴S△COD:S△BOE=1:4,S△COD:S四边形CDBE=1:3,
∴S△DOC=$\frac{1}{3}$,S△BOE=$\frac{4}{3}$,
则k=$\frac{8}{3}$.
点评 此题考查了反比例函数系数k的几何意义,熟练掌握k的几何意义是解本题的关键.

练习册系列答案
相关题目
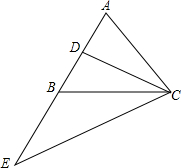 已知△ABC,AB=AC,AD=BD,AB=BE,求证:∠ACD=∠E.
已知△ABC,AB=AC,AD=BD,AB=BE,求证:∠ACD=∠E. 如图,校园内有两棵树,相距8米,一棵树树高AB=13米,另一棵树高CD=7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?
如图,校园内有两棵树,相距8米,一棵树树高AB=13米,另一棵树高CD=7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞多少米?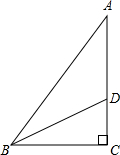 如图,在Rt△ABC中,∠C=90°,BD是三角形的角平分线,交AC于点D,AD=2.2cm,AC=3.7cm,则点D到AB边的距离是1.5cm.
如图,在Rt△ABC中,∠C=90°,BD是三角形的角平分线,交AC于点D,AD=2.2cm,AC=3.7cm,则点D到AB边的距离是1.5cm. 如图,D是AB的中点,E是BC的中点,BE=$\frac{1}{5}$AC=3cm,求线段DE的长.
如图,D是AB的中点,E是BC的中点,BE=$\frac{1}{5}$AC=3cm,求线段DE的长.