题目内容
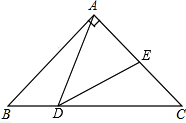 已知如图△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°,△ABD∽△DCE.当△ADE是等腰三角形时,求AE的长.
已知如图△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°,△ABD∽△DCE.当△ADE是等腰三角形时,求AE的长.考点:相似三角形的性质,等腰直角三角形
专题:
分析:当△ADE是等腰三角形时,因为三角形的腰和底不明确,所以应分AD=AE,AD=DE,AE=DE三种情况讨论.
解答: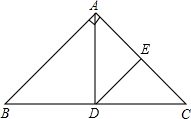 解:分三种情况:
解:分三种情况:
①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意;
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=1,BC=
,AE=AC-EC=1-BD=1-(
-1)=2-
;
③若AE=DE,此时∠DAE=∠ADE=45°,如图所示,
易知AD⊥BC,DE⊥AC,且AD=DC.
由等腰三角形的三线合一可知:AE=CE=
AC=
.
综上所述,当△ADE是等腰三角形时,AE的长为2-
或
.
 解:分三种情况:
解:分三种情况:①若AD=AE时,∠DAE=90°,此时D点与点B重合,不合题意;
②若AD=DE时,△ABD与△DCE的相似比为1,此时△ABD≌△DCE,
于是AB=AC=1,BC=
| 2 |
| 2 |
| 2 |
③若AE=DE,此时∠DAE=∠ADE=45°,如图所示,
易知AD⊥BC,DE⊥AC,且AD=DC.
由等腰三角形的三线合一可知:AE=CE=
| 1 |
| 2 |
| 1 |
| 2 |
综上所述,当△ADE是等腰三角形时,AE的长为2-
| 2 |
| 1 |
| 2 |
点评:此题考查了相似三角形的性质,等腰直角三角形的性质,等腰三角形的性质,难度适中,进行分类讨论是解题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
一次函数y=ax+b交x轴于点(-5,0),则关于x的方程ax+b=0的解是( )
| A、x=5 | B、x=-5 |
| C、x=0 | D、无法求解 |
 如图,△ABC为等腰直角三角形,AB=BC=2,点Q为BC的中点,P为边AC上一动点,求△PBQ周长的最小值.
如图,△ABC为等腰直角三角形,AB=BC=2,点Q为BC的中点,P为边AC上一动点,求△PBQ周长的最小值.