题目内容
如图，△ABC为等腰直角三角形，AB=BC=2，点Q为BC的中点，P为边AC上一动点，求△PBQ周长的最小值．考点：轴对称-最短路线问题
专题：
分析：作Q关于AC的对称点D，连接PQ，CD，则AC垂直平分QD，可得PQ=PD，CQ=CD，即可求得∠BCD=90°，根据勾股定理可得BD2=BC2+CD2，即可求得BD的值，即可解题．
解答：解：作Q关于AC的对称点D，连接PQ，CD，
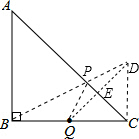
则AC垂直平分QD，
∴PQ=PD，CQ=CD=
BC=1，∠DCP=∠QCP，
∵△ABC为等腰直角三角形，AB=BC，
∴∠ACB=45°，
∴∠BCD=∠ACB+∠ACD=90°，
∴BD2=BC2+CD2=5，
∴BD=
，
∴△PBQ周长的最小值=BQ+BP+PQ=BQ+BD=1+
．
答：△PBQ周长的最小值为1+
．
则AC垂直平分QD，
∴PQ=PD，CQ=CD=
| 1 |
| 2 |
∵△ABC为等腰直角三角形，AB=BC，
∴∠ACB=45°，
∴∠BCD=∠ACB+∠ACD=90°，
∴BD2=BC2+CD2=5，
∴BD=
| 5 |
∴△PBQ周长的最小值=BQ+BP+PQ=BQ+BD=1+
| 5 |
答：△PBQ周长的最小值为1+
| 5 |
点评：本题考查了最短路线问题，考查了轴对称和垂直平分线的性质，本题中求得BD的长是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列问题中，两个变量成反比例函数的是（ ）
| A、正方形的周长C与它的边长a |
| B、除数一定，被除数和商 |
| C、三角形的面积一定，一边的长a与这边上的高h |
| D、每支铅笔0.5元，买铅笔的支数与总的价钱 |
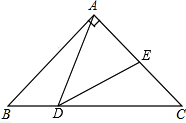已知如图△ABC中，∠BAC=90°，AB=AC=1，点D是BC边上的一个动点（不与B，C点重合），∠ADE=45°，△ABD∽△DCE．当△ADE是等腰三角形时，求AE的长．
我国在国际舞台始终注重主动承担国际责任，自2008年12月份起已先后向亚丁湾派出十四批次护航编队，共计四十余艘（次）战舰．2013年6月6日，第十四批护航编队中“微山湖”号综合补给舰从点A处准备靠岸补给休整，然后赶往B点继续执行护航任务，请给出其最佳停靠地点，使其航程最短．