如图.将一根25cm长的细木棒放入长.宽.高分别为8cm.6cm和$\sqrt{300}$cm的长方体无盖盒子中.则细木棒露在盒外面的最短长度是( )A．4cmB．5cmC．6cmD．7cm 题目和参考答案——青夏教育精英家教网—

题目内容

14．

如图，将一根25cm长的细木棒放入长、宽、高分别为8cm、6cm和$\sqrt{300}$cm的长方体无盖盒子中，则细木棒露在盒外面的最短长度是（　　）

A．

4cm

B．

5cm

C．

6cm

D．

7cm

分析由题意可知长方体对角线是最长的，当木条在盒子里对角放置的时候露在外面的长度最小，利用勾股定理求解即可．

解答解：由题意知：盒子底面对角长为$\sqrt{{6}^{2}+{8}^{2}}$=10（cm），
盒子的对角线长：$\sqrt{1{0}^{2}+（\sqrt{300}）^{2}}$=20（cm），
细木棒长25cm，故细木棒露在盒外面的最短长度是：25-20=5cm．
故选：B．

点评本题考查了勾股定理的应用，善于挖掘题目的隐含信息是解决本题的关键．

练习册系列答案

（1）求抛物线的解析式；
（2）联结AC、PC、BC、PB，试判断△AOC与△PCB是否相似？说明理由；
（3）过点P作PH⊥x轴于点H，在PH的右侧的抛物线上有一动点M（点M与顶点P不重合），过点M作MN⊥BP于点N，当△MPN与△BPH相似时，求点M的坐标．

5．已知⊙O的半径为5cm，若OP=3cm，那么点P与⊙O的位置关系是（　　）

2．

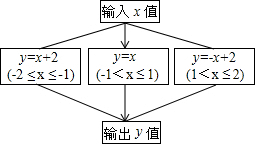根据如图所示的程序计算函数值，若输出的y值为-0.5，则输入的x值为-0.5．

9．解方程：
（1）3x-4（2x+5）=x+4
（2）x-$\frac{x-1}{2}$=2-$\frac{x+2}{3}$
（3）$\frac{x-1}{0.3}$-$\frac{x+2}{0.5}$=12．

19．（1）解方程：16x²-49=0；
（2）计算：$\sqrt{（-6）^{2}}$+$\root{3}{27}$-（$\sqrt{5}$）²．

6．

如图，一架云梯长25米，斜靠在一面墙上，梯子靠墙的一端距地面24米．
（1）这个梯子底端离墙有多少米？
（2）如果梯子的顶端下滑了4米，那么梯子的底部在水平方向也滑动了4米吗？
（3）若梯子的中点为P，则随着梯子位置的变化，点P到墙角的距离发生变化吗？若变化请说明变化趋势；若不变，请说明理由．

a²•a³=a⁶

a⁶÷a³=a²

4．已知代数式x²+ax+6-2bx²+x-1的值与字母x的取值无关，又A=-a²+ab-2b²，B=3a²-ab+3b²．求：3A+[（A+3B）-2（A+B）]的值．

试题分类