题目内容
11.(1)化简:$\frac{2\sqrt{2}×\sqrt{6}}{\sqrt{15}}$-$\frac{4\sqrt{2}}{\sqrt{10}}$(2)解方程组:$\left\{\begin{array}{l}{2x+3y=15}\\{5x+6y=35}\end{array}\right.$.
分析 (1)先根据二次根式的乘法法则得到原式=$\frac{2\sqrt{2}×\sqrt{2}×\sqrt{3}}{\sqrt{3}×\sqrt{5}}$-$\frac{4\sqrt{2}}{\sqrt{2}×\sqrt{5}}$,然后化简后合并即可;
(2)利用加减消元法先求出x,再利用代入法求出y即可.
解答 解:(1)原式=$\frac{2\sqrt{2}×\sqrt{2}×\sqrt{3}}{\sqrt{3}×\sqrt{5}}$-$\frac{4\sqrt{2}}{\sqrt{2}×\sqrt{5}}$
=$\frac{4\sqrt{5}}{5}$-$\frac{4\sqrt{5}}{5}$
=0;
(2)$\left\{\begin{array}{l}{2x+3y=15①}\\{5x+6y=35②}\end{array}\right.$,
①×2-②得4x-5x=30-35,
解得x=5,
把x=5代入①得10+3y=15,
解得y=$\frac{5}{3}$,
所以方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=\frac{5}{3}}\end{array}\right.$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了解二元一次方程组.

练习册系列答案
相关题目
1.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
19.下列各式中互为相反数的算式是( )
①-(-3)②(-3)2 ③|-(-3)|④-|-32|
①-(-3)②(-3)2 ③|-(-3)|④-|-32|
| A. | ①② | B. | ①③ | C. | ②④ | D. | ③④ |
20.多项式2xy-3xy2+25的次数及最高次项的系数分别是( )
| A. | 3,-3 | B. | 2,-3 | C. | 5,-3 | D. | 2,3 |
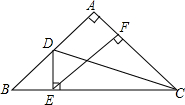 如图所示,在等腰直角三角形ABC中,∠A=90°,∠ACB的平分线CD交AB于点D,DE⊥BC于点E.
如图所示,在等腰直角三角形ABC中,∠A=90°,∠ACB的平分线CD交AB于点D,DE⊥BC于点E.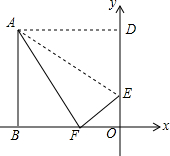 在平面直角坐标系中,长方形ODAB的边OB在x轴上,OD在y轴上,点O为原点,边OB=10,AB=8,将长方形沿AE翻折,使点D落在边OB上的点F处,则AE所在直线的表达式为y=-$\frac{1}{2}$x+3.
在平面直角坐标系中,长方形ODAB的边OB在x轴上,OD在y轴上,点O为原点,边OB=10,AB=8,将长方形沿AE翻折,使点D落在边OB上的点F处,则AE所在直线的表达式为y=-$\frac{1}{2}$x+3.