题目内容
17.若方程x2+mx+1=0的一个根是2,则m=-$\frac{5}{2}$.分析 把x=2代入已知方程,列出关于m的新方程,通过解新方程可以求得m的值.
解答 解:把x=2代入方程x2+mx+1=0,得
4+2m+1=0,
解得m=-$\frac{5}{2}$.
故答案是:-$\frac{5}{2}$.
点评 本题考查的是一元二次方程的根即方程的解的定义.一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
7.将抛物线y=(x-1)2+2沿x轴折叠后得到的新抛物线的解析式为( )
| A. | y=(x+1)2-2 | B. | y=(x-1)2-2 | C. | y=-(x-1)2+2 | D. | y=(x+1)2+2 |
7.使一元二次方程x2+3x+m=0有整数根的非负整数m的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
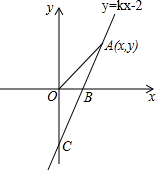 如图,直线y=kx-2与x轴,y轴分别交于B,C两点,其中OB=1.
如图,直线y=kx-2与x轴,y轴分别交于B,C两点,其中OB=1.