题目内容
13.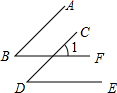 如图所示,AB∥CD,∠B=∠D,求证:BF∥DE(请在括号或横线上填空)
如图所示,AB∥CD,∠B=∠D,求证:BF∥DE(请在括号或横线上填空)证明:∵AB∥CD(已知)
∴∠B=∠1((两直线平行,同位角相等)
∵∠B=∠D(已知)
∴∠1=∠D(等量代换)
∴BF∥DE(同位角相等,两直线平行)
分析 根据平行线的性质由AB∥CD得到∠B=∠1,再利用等量代换得到∠1=∠D,然后根据平行线的判定方法可判断BF∥DE.
解答 证明:∵AB∥CD(已知),
∴∠B=∠1,(两直线平行,同位角相等),
∵∠B=∠D(已知),
∴∠1=∠D(等量代换),
∴BF∥DE(同位角相等,两直线平行).
故答案为已知;两直线平行,同位角相等;已知;等量代换;同位角相等,两直线平行.
点评 本题考查了平行线的判定与性质:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
4.具备下列条件的两个三角形中,不一定全等的是( )
| A. | 能够完全重合 | B. | 三边对应相等 | ||
| C. | 两角及一边对应相等 | D. | 两边及一角对应相等 |
1. 如图,已知AB∥CD,HL∥FG,EF⊥CD,∠1=50°,那么,∠EHL的度数为( )
如图,已知AB∥CD,HL∥FG,EF⊥CD,∠1=50°,那么,∠EHL的度数为( )
 如图,已知AB∥CD,HL∥FG,EF⊥CD,∠1=50°,那么,∠EHL的度数为( )
如图,已知AB∥CD,HL∥FG,EF⊥CD,∠1=50°,那么,∠EHL的度数为( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
3. 如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
 如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )
如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(-1,-2),“马”位于点(2,-2),则“兵”位于点( )| A. | (-1,1) | B. | (-2,-1) | C. | (-3,1) | D. | (1,-2) |
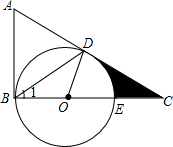 如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.
如图,在△ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.