题目内容

1．如图，已知AB∥CD，HL∥FG，EF⊥CD，∠1=50°，那么，∠EHL的度数为（　　）
A．40°B．45°C．50°D．55°

分析 利用平行线的性质可得∠GFD=∠1，∠EHL=∠EFG，又因为EF⊥CD，所以∠EFD=90°，即∠EFG+∠GFD=90°，结合已知，利用等量代换即可计算．

解答 解：∵AB∥CD，
∴∠GFD=∠1=50°
∵EF⊥CD，
∴∠EFD=90°，
∴∠EFG=90°-50°=40°．
又∵HL∥FG，
∴∠EHL=∠EFG=40°．
故选A．

点评 此题主要考查了平行线的性质，两直线平行时，应该想到角之间的数量关系，从而达到解决问题的目的．

练习册系列答案
相关题目
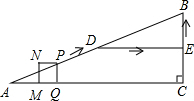11．如图，在Rt△ABC中，∠ACB=90°，AC=16cm，BC=12cm．D、E分别为边AB、BC的中点，连接DE．点P从点A出发，沿折线AD-DE-EB运动，到点B停止．点P在线段AD上以5cm/s的速度运动，在折线DE-EB上以1cm/s的速度运动．当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M在线段AQ上．设点P的运动时间为t（s）．
（1）当点P在线段DE上运动时，线段DP的长为t-2cm（用含t的代数式表示）．
（2）当点N落在AB边上时，求t的值．
（3）设正方形PQMN与△ABC重叠部分图形面积为S（cm2），直接写出S与t的函数关系式以及相应的自变量t的取值范围．
（4）连接CD，当点N与点D重合时，有一点H从点M出发，在线段MN上以6cm/s的速度沿M-N-M连续做往返运动，在点P的整个运动过程中，请你求出点H落在线段CD上时t的值．
12．若M-（-N）=0，则M与N的关系是（　　）
A．互为相反数B．大小相等C．M＞ND．M＜N
9．如图，已知∠1+∠2=180°，∠DAE=∠BCF．
（1）求证：AE∥CF；
（2）若∠BCF=70°，求∠ADF的度数．
16．已知：a+b+c=0，则（a+b）（b+c）（c+a）+abc的值为（　　）
A．-1B．0C．1D．-3
6．若am=3，an=2，则am-2n的值为（　　）
A．12B．6C．$\frac{3}{2}$D．$\frac{3}{4}$
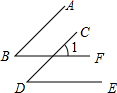13．如图所示，AB∥CD，∠B=∠D，求证：BF∥DE（请在括号或横线上填空）
证明：∵AB∥CD（已知）
∴∠B=∠1（（两直线平行，同位角相等）
∵∠B=∠D（已知）
∴∠1=∠D（等量代换）
∴BF∥DE（同位角相等，两直线平行）
10．先化简，再求值
（1-$\frac{1}{a-2}$）÷$\frac{a-2}{{a}^{2}-4}$，其中a=-3．
11．若关于x的一元二次方程x2-4x-k=0有两个实数根，则（　　）
A．k＞4B．k＞-4C．k≥4D．k≥-4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网