题目内容
16.有一列式子,按照一定的规律排列成-3a2,9a5,-27a10,81a17,-243a26…,则第n个式子为$(-3)^{n}{a}^{{n}^{2}+1}$(n为正整数).分析 利用归纳法来求已知数列的通式.
解答 解:∵第一个式子:-3a2=$(-3)^{1}{a}^{{1}^{2}+1}$,
第二个式子:9a5=$(-3)^{2}{a}^{{2}^{2}+1}$,
第三个式子:-27a10=$(-3)^{3}{a}^{{3}^{2}+1}$,
第四个式子:81a17=$(-3)^{4}{a}^{{4}^{2}+1}$,
….
则第n个式子为:$(-3)^{n}{a}^{{n}^{2}+1}$(n为正整数).
故答案是:$(-3)^{n}{a}^{{n}^{2}+1}$.
点评 本题考查了单项式.此题的解题关键是找出该数列的通式.

练习册系列答案
相关题目
6.下列函数中,是y关于x的反比例函数的是( )
| A. | y=2x | B. | y=$\frac{3}{2x}$ | C. | y=$\frac{2}{x-1}$ | D. | y=$\frac{2}{x}$-1 |
7.“五一”旅游黄金周期间,几名同学包租一辆面包车前往某景区游玩,面包车的租价为180元,出发时,又增加了2名学生,结果每个同学比原来少分担3元车费.设参加游玩的同学为x人,则可得方程( )
| A. | $\frac{180}{x}$-$\frac{180}{x+2}$=2 | B. | $\frac{180}{x+2}$-$\frac{180}{x}$=3 | C. | $\frac{180}{x}$-$\frac{180}{x-2}$=3 | D. | $\frac{180}{x-2}$-$\frac{180}{x}$=3 |
 已知一次函数y=-2x+7的图象与x轴、y轴分别交于点A、B.
已知一次函数y=-2x+7的图象与x轴、y轴分别交于点A、B.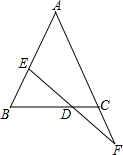 已知:如图,D是EF的中点,BE=CF,求证:△ABC是等腰三角形.
已知:如图,D是EF的中点,BE=CF,求证:△ABC是等腰三角形.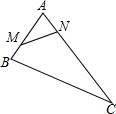 如图,在△ABC中,AB=8,AC=16,点M从点B开始沿BA边向点A以2个单位长度/秒的速度移动,点N从点A开始沿AC边向点C以4个单位长度/秒的速度移动.如果点M、N分别从点B、A同时出发,移动几秒,△AMN与△ABC相似?
如图,在△ABC中,AB=8,AC=16,点M从点B开始沿BA边向点A以2个单位长度/秒的速度移动,点N从点A开始沿AC边向点C以4个单位长度/秒的速度移动.如果点M、N分别从点B、A同时出发,移动几秒,△AMN与△ABC相似?