题目内容
17.已知$x+\frac{1}{x}=\sqrt{10}$,求x2+$\frac{1}{{x}^{2}}$的值,其结果是8.分析 把已知等式两边平方,利用完全平方公式化简,即可求出所求式子的值.
解答 解:把x+$\frac{1}{x}$=$\sqrt{10}$,两边平方得:(x+$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$+2=10,
整理得:x2+$\frac{1}{{x}^{2}}$=8,
故答案为:8.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
12.已知直角三角形两边的长分别为5、12,则第三边的长为( )
| A. | 13 | B. | 60 | C. | 17 | D. | 13或$\sqrt{119}$ |
9.下列方程中,其解为-2的是( )
| A. | $\frac{x+5}{3}-1=0$ | B. | 3(x+1)-3=0 | C. | 3x-4=2 | D. | 2x=-1 |
7.如果x2-(m-1)x+1是一个完全平方式,则m的值为( )
| A. | -1 | B. | 1 | C. | -1或3 | D. | 1或3 |
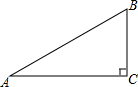 已知:如图Rt△ABC中,∠C=90°,AC=$\sqrt{7}$+1,BC=$\sqrt{7}$-1.求:
已知:如图Rt△ABC中,∠C=90°,AC=$\sqrt{7}$+1,BC=$\sqrt{7}$-1.求: 如图,已知直线AD,BE相交于点O,∠BOC=90°,OF平分∠AOE,若∠1=35°,求∠2,∠3和∠DOF的度数.
如图,已知直线AD,BE相交于点O,∠BOC=90°,OF平分∠AOE,若∠1=35°,求∠2,∠3和∠DOF的度数.