题目内容
5.已知a2b2+a2+b2+1=-4ab,求a2+b2的值.(提示:将-4ab移到左边,然后分组分解)分析 利用配方法把a2b2+a2+b2+1=-4ab变形为(ab+1)2+(a+b)2=0,根据非负数的性质以及a2+b2=(a+b)2-2ab即可解决问题.
解答 解:∵a2b2+a2+b2+1=-4ab,
∴(a2b2+2ab+1)+(a2+2ab+b2)=0,
∴(ab+1)2+(a+b)2=0,
∵(ab+1)2≥0,(a+b)2≥0,
∴ab=-1,a+b=0
∴a2+b2=(a+b)2-2ab=2.
点评 本题考查因式分解的应用、完全平方公式等知识,解题的关键是灵活运用配方法将等式恒等变形,巧用非负数的性质解决问题,属于中考常考题型.

练习册系列答案
相关题目
13.政府去年对某校的投资为2百万元,预计今明两年的投资总额为8百万元,设政府对该校这两年投资的平均增长率为x,则可列方程为( )
| A. | 2(1+x)2=4 | B. | 2(1+x)2=8 | C. | 2(x+2)2=8 | D. | 2(x+1)(x+2)=8 |
17.在下列各选项中给出的三条线段不一定能组成三角形的是( )
| A. | a+1,a+2,a+3(a>0) | B. | 三条线段的比是4:6:8 | ||
| C. | 3cm,8cm,10cm | D. | 3a,5a,2a+1(a>0) |
16. 如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
 如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )| A. | 相等 | B. | 互余 | C. | 互补 | D. | 无法确定 |
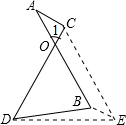 如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明原因.
如图,线段AB=CD,AB与CD相交于点O,且∠1=60°,CE是由AB平移所得,试确定AC+BD与AB的大小关系,并说明原因. 如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E.
如图,正方形ABCD中,AC,BD相交于点O,AE平分∠BAC交BD于E.