题目内容
5.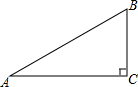 已知:如图Rt△ABC中,∠C=90°,AC=$\sqrt{7}$+1,BC=$\sqrt{7}$-1.求:
已知:如图Rt△ABC中,∠C=90°,AC=$\sqrt{7}$+1,BC=$\sqrt{7}$-1.求:(1)Rt△ABC的面积;
(2)斜边AB的长.
分析 (1)由三角形的面积公式直接计算即可;
(2)根据勾股定理来求AB的长度即可.
解答 解:(1)S△=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×($\sqrt{7}$+1)($\sqrt{7}$-1)=3;
(2)由勾股定理得:AB2=AC2+BC2=($\sqrt{7}$+1)2+($\sqrt{7}$-1)2=16,即AB=4.
点评 本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方(如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2).

练习册系列答案
相关题目
13.政府去年对某校的投资为2百万元,预计今明两年的投资总额为8百万元,设政府对该校这两年投资的平均增长率为x,则可列方程为( )
| A. | 2(1+x)2=4 | B. | 2(1+x)2=8 | C. | 2(x+2)2=8 | D. | 2(x+1)(x+2)=8 |
16. 如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
 如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )| A. | 相等 | B. | 互余 | C. | 互补 | D. | 无法确定 |
10.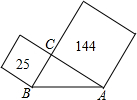 如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
 如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )
如图,已知在直角三角形ABC中,以直角边BC、AC为边的正方形的面积分别为25、144,则AB的长为( )| A. | 169 | B. | 119 | C. | 13 | D. | 17 |