题目内容
8.计算:①1+2-3-4+5+6-7-8+9+…-2012+2013+2014-2015-2016+2017=1;
②1-22+32-42+52-…-962+972-982+992=4950.
分析 ①通过观察题目可以发现,每相邻的四项的和为-4,题目中前2016项除以4可以得到有多少组,从而可以解答本题;
②充分利用平方差公式对原式进行分解,然后根据第一个与最后一组的和可以求得前98项的和然后再与第99项相加即可解答本题.
解答 解:①1+2-3-4+5+6-7-8+9+…-2012+2013+2014-2015-2016+2017
=(1+2-3-4)+(5+6-7-8)+…+(2013--2014-2015-2016)+2017
=(-4)×(2016÷4)+2017
=(-4)×504+2017
=-2016+2017
=1;
②1-22+32-42+52-…-962+972-982+992
=(1-2)(1+2)+(3-4)(3+4)+…+(97-98)(97+98)+992
=(-3)+(-7)+…+(-195)+992
=[(-3)+(-195)]×24+(-99)+9801
=4950;
故答案为:1;4950.
点评 本题考查有理数的混合运算、平方差公式,解题的关键是明确题意,通过观察式子可以发现其中的规律,巧妙的利用平方差公式,进行正确的分组.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.在下列各选项中给出的三条线段不一定能组成三角形的是( )
| A. | a+1,a+2,a+3(a>0) | B. | 三条线段的比是4:6:8 | ||
| C. | 3cm,8cm,10cm | D. | 3a,5a,2a+1(a>0) |
16. 如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
 如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )
如图,四边形ABCD是⊙O的内接四边形,∠DAB与∠DCE的关系是( )| A. | 相等 | B. | 互余 | C. | 互补 | D. | 无法确定 |
3.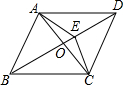 如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )
如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )
 如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )
如图,在菱形ABCD中,∠ABC=70°,AC与BD相交于点O,E是OD上一点,若有AE=DE,则下列说法不正确的是( )| A. | 点E是△ACD的内心 | B. | ∠DBC=35° | C. | CE=DE | D. | △ABO≌△CBO |
18. 如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
 如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )
如图,在△ABC中,∠ACB=90°,D为AB的中点,E为AC上一点,连接DE,并过点D作FD⊥ED,垂足为D,交BC于点F.若AC=BC=14,AE:EC=4:3,则tan∠EFC的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{4}$ |