题目内容
6.现有一矩形ABCD和一等腰直角三角形BEF按如图1所示的位置放置(AB和BE重合),其中AB=25,AD=48,将△BEF绕点B顺时针旋转α°(0<α<90),在旋转过程中,EF与AD交于点G,如图2所示.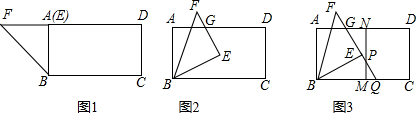
(1)求证:AG=EG;
(2)连接CE、DE,试判断是否存在以DE为腰的等腰三角形CDE,若存在,请求出此时α的度数;若不存在,请说明理由;
(3)如图3,以AB为边在矩形内部作正方形ABMN,直角边EF所在的直线交MN于点P,交BC于点Q,设AG=x,PN=y,写出y关于x的函数关系式.
分析 (1)连接BG,证明Rt△BAG≌Rt△BEG,根据全等三角形的性质证明结论;
(2)分DE=CD、DE=CE两种情况,根据三角形三边关系以及等腰三角形的性质解答即可;
(3)证明Rt△BEP≌Rt△BMP,得到EP=MP,同理得到AG=EG,用x表示出GN,根据勾股定理列出y关于x的函数关系式.
解答 解:(1)如图2,连接BG,
在Rt△BAG和Rt△BEG中,
$\left\{\begin{array}{l}{AB=BE}\\{BG=BG}\end{array}\right.$,
∴Rt△BAG≌Rt△BEG,
∴AG=EG;
(2)存在.
当DE=CD时,可知DE=25,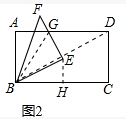
连接BD,在Rt△BCD中,BD2=BC2+CD2=2929,
∴BE+DE=25+25=50<$\sqrt{2929}$,
即不存在△BDE,
∴不可能出现DE=CD.
当DE=CE时,可知点E在CD的垂直平分线上,
过点E作EH⊥BC于点H,
∴EH=$\frac{25}{2}$.
在Rt△BEH中,BE=25,EH=$\frac{25}{2}$,
∴∠EBH=30°,
∴∠ABE=60°.
综上所述,存在以DE为腰的等腰三角形CDE,此时α的度数为60°.
(3)如图3,连接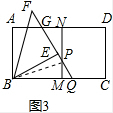 BP,
BP,
在Rt△BEP和Rt△BMP中,
$\left\{\begin{array}{l}{BE=BM}\\{BP=BP}\end{array}\right.$,
∴Rt△BEP≌Rt△BMP,
∴EP=MP,
同理,AG=EG,
∵PN=y,
∴EP=MP=25-y.
∵AG=EG,
∴GP=x+25-y.
在Rt△GNP中,∵GN=25-x,NP=y,
∴y2+(25-x)2=(x+25-y)2,
化简,得y=$\frac{50x}{25+x}$.
点评 本题考查的是正方形的性质、等腰直角三角形的性质、等腰三角形的性质以及函数解析式的确定,掌握相关的性质定理、灵活运用数形结合思想是解题的关键,注意勾股定理的应用.

| A. | 2的倍数,但不一定是4的倍数 | B. | 4的倍数,但不一定是8的倍数 | ||
| C. | 8的倍数,但不一定是16的倍数 | D. | 16的倍数,但不一定是32的倍数 |
| A. |  | B. |  | C. |  | D. |  |
 如图所示,实数a=$\sqrt{3}$,则在数轴上,表示-a的点应落在( )
如图所示,实数a=$\sqrt{3}$,则在数轴上,表示-a的点应落在( )| A. | 线段AB上 | B. | 线段BC上 | C. | 线段CD上 | D. | 线段DE上 |