题目内容
3．
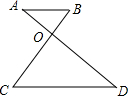如图，线段AD与BC相交于点O，AB∥CD，若AB：CD=2：3，△ABO的面积是2，则△CDO的面积等于4.5．
分析 根据AB∥CD，于是得到△ABO∽△CDO，然后根据相似三角形面积的比等于相似比的平方即可得到结论．
解答 解：∵AB∥CD，
∴△ABO∽△CDO，
∴$\frac{{S}_{△ABO}}{{S}_{△CDO}}$=（$\frac{AB}{CD}$）2=（$\frac{2}{3}$）2=$\frac{4}{9}$，
∵△ABO的面积是2，
∴△CDO的面积等于4.5．
故答案为：4.5．
点评 本题考查的是相似三角形的判定与性质，熟知相似三角形面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
13．近阶段潍坊持续干旱，给居民生活带来不便，关注水龙头的浪费十分必要，假设20滴水1毫升，一分钟浪费60滴，一年按365天计算，一年浪费水的质量用科学记数法表示为（ ）克（保留3个有效数字）
| A． | 1.60×106 | B． | 1.57×106 | C． | 1.58×106 | D． | 1.58×105 |
14．某种品牌运动服经过两次降价，每件零件售价由640元将为360元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（ ）
| A． | 360（1+x）2=640 | B． | 640（1-x）2=360 | C． | 640（1-2x）2=360 | D． | 640（1-x2）=360 |
11．在0，-2，2，-3这四个数中，最小的数是（ ）
| A． | 0 | B． | -2 | C． | 1 | D． | -3 |
如图，在8×5的正方形网格中，每个小正方形的边长都为1，点A在格点（网格线的交点）上，且点A的坐标为（0，4）．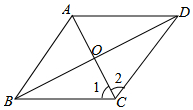
如图，菱形ABCD对角线AC，BD相交于点O，有下列结论：
12．一组数据2、9、5、5、8、5、8的中位数是（ ）
| A． | 2 | B． | 5 | C． | 8 | D． | 9 |
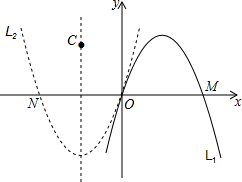在直角坐标系xOy中，定义点C（a，b）为抛物线L：y=ax2+bx（a≠0）的特征点坐标．