题目内容
8.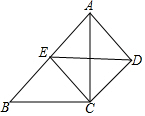 如图,CD∥AB,且CD=$\frac{1}{2}$AB,点E为AB的中点,若四边形ADCE为正方形,则∠B=45°.
如图,CD∥AB,且CD=$\frac{1}{2}$AB,点E为AB的中点,若四边形ADCE为正方形,则∠B=45°.
分析 根据题意证得四边形BCDE为平行四边形,即可证得∠B=∠EDC,根据正方形的性质证得∠EDC=$\frac{1}{2}$∠ADC=45°,从而证得∠B=45°.
解答 证明:∵CD=$\frac{1}{2}$AB,点E为AB的中点,
∴CD=BE,
∵CD∥AB,
∴四边形BCDE为平行四边形,
∴∠B=∠EDC,
∵四边形ADCE为正方形,
∴∠EDC=$\frac{1}{2}$∠ADC=45°,
∴∠B=45°.
故答案为45°.
点评 本题考查了平行四边形的判定和性质,正方形的性质等,熟练掌握性质定理上解题的关键.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
18. 如图所示,实数a、b在数轴上的位置,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{(b-1)^{2}}$=( )
如图所示,实数a、b在数轴上的位置,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{(b-1)^{2}}$=( )
 如图所示,实数a、b在数轴上的位置,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{(b-1)^{2}}$=( )
如图所示,实数a、b在数轴上的位置,化简:$\sqrt{(a-b)^{2}}$-$\sqrt{{a}^{2}}$-$\sqrt{(b-1)^{2}}$=( )| A. | 2b-2a-1 | B. | -2a+1 | C. | 1 | D. | 2b-1 |
7.中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数,如果收入1000元记作+1000元,那么-800表示( )
| A. | 支出800元 | B. | 收入800元 | C. | 支出200元 | D. | 收入200元 |
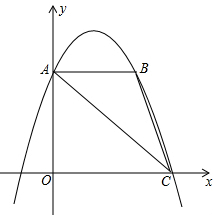 如图,已知抛物线y=-x2+bx+c经过点A(0,3),C(3,0);过A作AB∥x轴交抛物线于点B,连接AC、BC,点P为抛物线上动点.
如图,已知抛物线y=-x2+bx+c经过点A(0,3),C(3,0);过A作AB∥x轴交抛物线于点B,连接AC、BC,点P为抛物线上动点.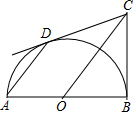 如图所示,AB是半圆O的直径,∠ABC=90°,点D是半圆O上一动点(不与点A、B重合),且AD∥CO.
如图所示,AB是半圆O的直径,∠ABC=90°,点D是半圆O上一动点(不与点A、B重合),且AD∥CO.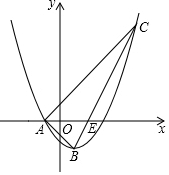 如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.
如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B.点C(5,m)在抛物线上,直线BC交x轴于点E.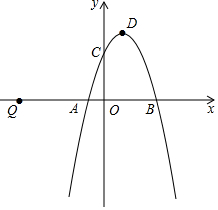 如图,二次函数y=mx2+(m2-m)x-2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.
如图,二次函数y=mx2+(m2-m)x-2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.