题目内容
3.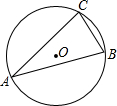 如图,⊙的半径为13cm,若tan∠CAB=$\frac{2}{3}$,那么BC=4$\sqrt{13}$;在本图中,若BC=6,sin∠CAB=$\frac{2}{3}$,那么⊙的半径为9.
如图,⊙的半径为13cm,若tan∠CAB=$\frac{2}{3}$,那么BC=4$\sqrt{13}$;在本图中,若BC=6,sin∠CAB=$\frac{2}{3}$,那么⊙的半径为9.
分析 连接CO并延长交⊙O于D,连接BD,则CD是⊙O的直径,于是得到CD=13×2=26,∠DBC=90°,然后解直角三角形即可得到结论.
解答 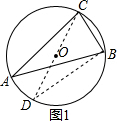 解:连接CO并延长交⊙O于D,连接BD,
解:连接CO并延长交⊙O于D,连接BD,
则CD是⊙O的直径,
∴CD=13×2=26,∠DBC=90°,
∵tan∠CAB=$\frac{2}{3}$,
∴$\frac{BC}{BD}$=$\frac{2}{3}$,
设BC=2k.BD=3k,
∴(2k)2+(3k)2=262,
∴k=2$\sqrt{13}$,
∴BC=4$\sqrt{13}$;
当BC=6,sin∠CAB=$\frac{2}{3}$,
∴$\frac{BC}{CD}$=$\frac{2}{3}$,
∴CD=18,
∴⊙O的半径为:9,
故答案为:4$\sqrt{13}$,9.
点评 本题考查了圆周角定理,解直角三角形,正确的作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
8.已知△ABC,若存在点D使以A、B、C、D为顶点的四边形是平行四边形,则这样点D有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4 |
15.在?ABCD中,∠A=36°,则∠C:∠B的值为( )
| A. | 1:3 | B. | 3:1 | C. | 4:1 | D. | 1:4 |
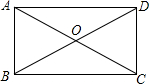 在矩形ABCD中,AC与BD交于点O,∠BOC=120°,AD=6cm,求AC的长.
在矩形ABCD中,AC与BD交于点O,∠BOC=120°,AD=6cm,求AC的长.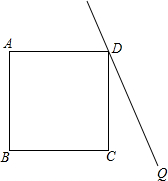 如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.
如图,在正方形ABCD外侧作直线DQ,点C关于直线DQ的对称点为P,连接DP、AP,AP交直线DQ于点F,交BD于点E.