题目内容
5．
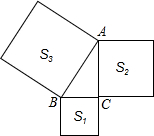如图所示，以Rt△ABC的三边向外作正方形，其面积分别为S1，S2，S3且S1=4，S2=8，则S3=（ ）| A． | 4 | B． | 8 | C． | 12 | D． | 32 |
分析 由正方形的面积公式可知S1=BC2，S2=AC2，S3=AB2，在Rt△ABC中，由勾股定理得AC2+BC2=AB2，即S1+S2=S3，由此可求S3．
解答 解：∵S1=4，
∴BC2=4，
∵S2=12，
∴AC2=8，
∴在Rt△ABC中，BC2+AC2=AB2=4+8=12，
∴S3=AB2=12．
故选：C．
点评 本题考查了勾股定理及正方形面积公式的运用，解题关键是明确直角三角形的边长的平方即为相应的正方形的面积，难度一般．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
完成下面的证明．
16．某城市用电收费实行阶梯电价，收费标准如下表所示，用户5月份交电费45元，则所用电量为20度．
| 月用电量 | 不超过12度的部分 | 超过12度不超过18度的部分 | 超过18度的部分 |
| 收费标准（元/度） | 2.00 | 2.50 | 3.00 |
13．已知实数x、y、z满足：（x+z）2-4（x-y）（y+z）=0，下列式子一定成立的是（ ）
| A． | x+y-z=0 | B． | x+y+2z=0 | C． | y-z-2x=0 | D． | -z+x-2y=0 |
20．在△ABD与△ACD中，∠BAD=∠CAD，且B点，C点在AD边两侧，则不一定能使△ABD和△ACD全等的条件是（ ）
| A． | BD=CD | B． | ∠B=∠C | C． | AB=AC | D． | ∠BDA=∠CDA |
10．
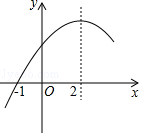二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①4a+b=0；②9a+c＞3b；③a+b+c＞0；④当x＞-1时，y的值随x值的增大而增大．其中正确的结论有（ ）
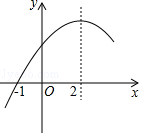二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①4a+b=0；②9a+c＞3b；③a+b+c＞0；④当x＞-1时，y的值随x值的增大而增大．其中正确的结论有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
17．
如图，下列各数中，数轴上点A表示的数可能是（ ）
如图，下列各数中，数轴上点A表示的数可能是（ ）| A． | 4的算术平方根 | B． | 4的立方根 | C． | 4的平方根 | D． | 8的算术平方根 |
14．传统佳节“春节”临近，剪纸民俗魅力四射，对称现象无处不在．观察下面的四幅剪纸，其中是轴对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
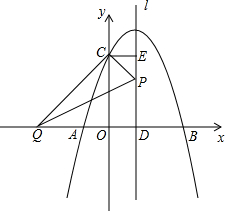如图，二次函数y=ax2+bx+c的图象与x轴交于点A（-1，0）、B（3，0），与y轴交于点C（0，3）．