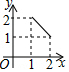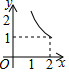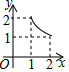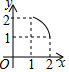题目内容
2. 完成下面的证明.
完成下面的证明.已知:如图,BC∥DE,BE、DF分别是∠ABC、∠ADE的平分线.求证:∠1=∠2.
分析 根据平行线的性质得出∠ABC=∠ADE,根据角平分线定义得出∠3=$\frac{1}{2}$∠ABC,∠4=$\frac{1}{2}$∠ADE,求出∠3=∠4,根据平行线的判定得出DF∥BE,根据平行线的性质得出即可.
解答 证明:∵BC∥DE,
∴∠ABC=∠ADE.
∵BE、DF分别是∠ABC、∠ADE的平分线.
∴∠3=$\frac{1}{2}$∠ABC,∠4=$\frac{1}{2}$∠ADE,
∴∠3=∠4,
∴DF∥BE,
∴∠1=∠2.
点评 本题考查了平行线的性质,用到的知识点为:两直线平行,同位角相等,内错角相等.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
10.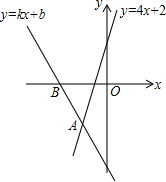 如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b的解集为( )
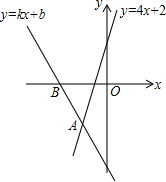 如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b的解集为( )
如图,经过点B(-2,0)的直线y=kx+b与直线y=4x+2相交于点A(-1,-2),则不等式4x+2<kx+b的解集为( )| A. | x<-2 | B. | x>-1 | C. | x<-1 | D. | x>-2 |
7.二元一次方程2x-y=-1与x+2y=12所对应直线的交点坐标是( )
| A. | (-1,-1) | B. | (2,5) | C. | (1,6) | D. | (-2,5) |
7.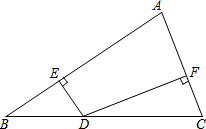 如图,在△ABC中,AB=20cm,AC=12cm,点D在BC边上,作DE⊥AB于E、DF⊥AC于F,若DE=5cm,△ABC的面积为122cm2,则DF的长为( )
如图,在△ABC中,AB=20cm,AC=12cm,点D在BC边上,作DE⊥AB于E、DF⊥AC于F,若DE=5cm,△ABC的面积为122cm2,则DF的长为( )
 如图,在△ABC中,AB=20cm,AC=12cm,点D在BC边上,作DE⊥AB于E、DF⊥AC于F,若DE=5cm,△ABC的面积为122cm2,则DF的长为( )
如图,在△ABC中,AB=20cm,AC=12cm,点D在BC边上,作DE⊥AB于E、DF⊥AC于F,若DE=5cm,△ABC的面积为122cm2,则DF的长为( )| A. | 9 cm | B. | 10 cm | C. | 11 cm | D. | 12 cm |
4. 如图所示的几何体,从正面看到所得的图形是( )
如图所示的几何体,从正面看到所得的图形是( )
 如图所示的几何体,从正面看到所得的图形是( )
如图所示的几何体,从正面看到所得的图形是( )| A. |  | B. |  | C. |  | D. |  |
5.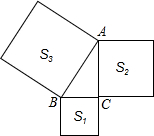 如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=( )
如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=( )
 如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=( )
如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=( )| A. | 4 | B. | 8 | C. | 12 | D. | 32 |
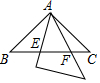 如图,两个全等的等腰直角三角板(斜边长为2)如图放置,其中一块三角板45°角的顶点与另一块三角板ABC的直角顶点A重合.若三角板ABC固定,当另一个三角板绕点A旋转时,它的直角边和斜边所在的直线分别与边BC交于点E、F.设BF=x,CE=y,则y关于x的函数图象大致是( )
如图,两个全等的等腰直角三角板(斜边长为2)如图放置,其中一块三角板45°角的顶点与另一块三角板ABC的直角顶点A重合.若三角板ABC固定,当另一个三角板绕点A旋转时,它的直角边和斜边所在的直线分别与边BC交于点E、F.设BF=x,CE=y,则y关于x的函数图象大致是( )