题目内容
3.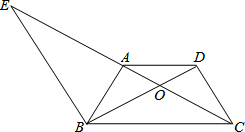 如图,等腰梯形ABCD中,AD∥BC,对角线AC、BD交于点O,过点B作BE∥CD交CA的延长线于E.
如图,等腰梯形ABCD中,AD∥BC,对角线AC、BD交于点O,过点B作BE∥CD交CA的延长线于E.(1)求证:OC2=OA•OE;
(2)若BD=6,OE=13,求OA、AE的值?
分析 (1)由平行线分线段成比例可得对应线段成比例,进而通过线段之间的转化即可得出结论;
(2)根据等腰梯形的性质得到AC=BD=6,设OA=x,则OC=6-x,由(1)知,OC2=OA•OE,列方程即可得到结果.
解答 (1)证明:∵AD∥BC,∴$\frac{OA}{OC}=\frac{OD}{OB}$,
又∵BE∥CD,∴$\frac{OD}{OB}$=$\frac{OC}{OE}$,
∴$\frac{OA}{OC}$=$\frac{OC}{OE}$,
即OC2=OA•OE;
(2)等腰梯形ABCD中,
∵AC=BD=6,
设OA=x,则OC=6-x,
中(1)知,OC2=OA•OE,
∴(6-x)2=13x,
解得:x=$\frac{25+\sqrt{481}}{2}$(不合题意,舍去),x=$\frac{25-\sqrt{481}}{2}$,
∴OA=$\frac{25-\sqrt{481}}{2}$,AE=OE-OA=$\frac{\sqrt{481}+1}{2}$.
点评 本题考查了相似三角形的判定与性质,梯形的性质.关键是由平行线得相似三角形和相等的比.

练习册系列答案
相关题目
13.下列给出的四个命题:①所有锐角三角函数值都是正数;②sin30°+sin60°=sin90°;③△ABC中,∠C=90°,若$sinA=\frac{3}{5}$,则a=3,c=5,其中真命题有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.已知函数y=|(x-1)2-1|,则使y=k成立的x值恰好有三个,则k的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.2014年北京APEC会议期间共有2280名青年志愿者上岗服务,2280用科学记数法表示为( )
| A. | 0.228×104 | B. | 2.28×102 | C. | 2.28×103 | D. | 2.28×104 |