题目内容
3.计算:(1)$3\sqrt{2}-2\sqrt{12}-4\sqrt{\frac{1}{8}}+3\sqrt{48}$
(2)${(1-\sqrt{3})^2}-{(\frac{1}{2})^{-1}}+\frac{4}{{\sqrt{3}+1}}+{(\sqrt{2}-1)^0}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)根据零指数幂和负整数指数幂的意义得到原式=1-2$\sqrt{3}$+3-2+2($\sqrt{3}$-1)+1,然后去括号后合并即可.
解答 解:(1)原式=3$\sqrt{2}$-4$\sqrt{3}$-$\sqrt{2}$+12$\sqrt{3}$
=2$\sqrt{2}$+8$\sqrt{3}$;
(2)原式=1-2$\sqrt{3}$+3-2+2($\sqrt{3}$-1)+1
=1-2$\sqrt{3}$+3-2+2$\sqrt{3}$-2+1
=1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.

练习册系列答案
相关题目
13.下列运算正确的是( )
| A. | 2$\sqrt{2}×\sqrt{2}=4$ | B. | 2a3•a4=2a7 | C. | (2a4)3=8a7 | D. | a8÷a2=a4 |
12.已知直线y=kx+b,若k+b<0,kb>0,那么该直线不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.点A(cos30°,-sin30°)关于y轴对称的点的坐标是( )
| A. | ($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | C. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) | D. | ($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) |
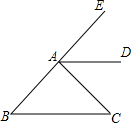 如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.
如图,AD是∠EAC的平分线,∠B=∠EAD,求证:∠B=∠C.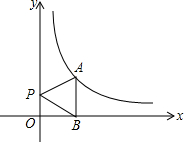 已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,
已知点A(m、n)是反比例函数$y=\frac{4}{x}$(x>0)的图象上一点,过A作AB⊥x轴于点B,P是y轴上一点,