题目内容
5. 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=10,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则半径r的取值范围是:2$\sqrt{5}$≤r<10.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=10,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.若⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,则半径r的取值范围是:2$\sqrt{5}$≤r<10.
分析 首先证明AB=AC,再根据已知得出Q在AC的垂直平分线上,作出线段AC的垂直平分线MN,作OE⊥MN,求出OE<r,求出r范围即可.
解答 解:连接OB.如图1,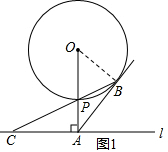
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC,
作出线段AC的垂直平分线MN,作OE⊥MN,如图2,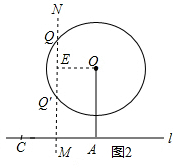
∴OE=$\frac{1}{2}$AC=$\frac{1}{2}$AB=$\frac{1}{2}$$\sqrt{{10}^{2}-{r}^{2}}$,
又∵圆O与直线MN有交点,
∴OE=$\frac{1}{2}$$\sqrt{{10}^{2}-{r}^{2}}$≤r,
∴$\sqrt{{10}^{2}-{r}^{2}}$≤2r,
即:100-r2≤4r2,
∴r2≥20,
∴r≥2$\sqrt{5}$.
∵OA=10,直线l与⊙O相离,
∴r<10,
∴2$\sqrt{5}$≤r<10.
故答案为:2$\sqrt{5}$≤r<10.
点评 本题考查了等腰三角形的性质和判定,相似三角形的性质和判定,切线的性质,勾股定理,直线与圆的位置关系等知识点的应用,主要培养学生运用性质进行推理和计算的能力.本题综合性比较强,有一定的难度.

练习册系列答案
相关题目
15.下列关于x的一元二次方程中一定有实数根的是( )
| A. | x2-2x+4=0 | B. | x2+2x+4=0 | C. | x2-2x-4=0 | D. | x2+4=0 |
13.面积为0.9m2的正方形地砖,它的边长介于( )
| A. | 90cm与100cm之间 | B. | 80cm与90cm之间 | C. | 70cm与80cm之间 | D. | 60cm与70cm之间 |
20.下列命题是假命题的是( )
| A. | 平行四边形的对边相等 | |
| B. | 对角线互相平分的四边形是平行四边形 | |
| C. | 四条边都相等的四边形是菱形 | |
| D. | 矩形的对角线互相垂直 |
20. 如图,∠AOC+∠BOC=90°,∠BOC与∠BOD互余,那么∠AOC与∠BOD的关系( )
如图,∠AOC+∠BOC=90°,∠BOC与∠BOD互余,那么∠AOC与∠BOD的关系( )
 如图,∠AOC+∠BOC=90°,∠BOC与∠BOD互余,那么∠AOC与∠BOD的关系( )
如图,∠AOC+∠BOC=90°,∠BOC与∠BOD互余,那么∠AOC与∠BOD的关系( )| A. | 互余 | B. | 互补 | C. | 相等 | D. | 不能确定 |
 将如图所示的A、B两组扑克牌分别洗匀后,背面朝上放置在桌面上.若分别从A、B两组牌中各随机抽取1张牌,求抽到2张牌的牌面数字之和是偶数的概率(用树状图或列表法求解).
将如图所示的A、B两组扑克牌分别洗匀后,背面朝上放置在桌面上.若分别从A、B两组牌中各随机抽取1张牌,求抽到2张牌的牌面数字之和是偶数的概率(用树状图或列表法求解).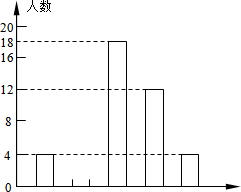 某校初三(1)班进行了一次跳绳测试,其中有8%的同学在17分以下,而且满分同学中只有1位男同学.体育委员将跳绳测试的统计结果绘制成如下的统计图,以便根据班级情况进行针对性训练.请你结合图中所给信息解答下列问题:
某校初三(1)班进行了一次跳绳测试,其中有8%的同学在17分以下,而且满分同学中只有1位男同学.体育委员将跳绳测试的统计结果绘制成如下的统计图,以便根据班级情况进行针对性训练.请你结合图中所给信息解答下列问题: