题目内容
8. 如图,AB∥CD,BE⊥DE,∠B=52°,试确定∠D的度数并说明理由.
如图,AB∥CD,BE⊥DE,∠B=52°,试确定∠D的度数并说明理由.
分析 首先过点E作EF∥AB,由AB∥CD,即可得EF∥AB∥CD,根据两直线平行,内错角相等,即可得∠1=∠B,∠2=∠D,又由BE⊥DE,即可求得∠B与∠D互余.
解答 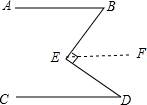 解:∠B+∠D=90°.
解:∠B+∠D=90°.
理由:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠1=∠B,∠2=∠D,
∵BE⊥DE,
∴∠1+∠2=90°,
∴∠B+∠D=90°,
∴∠D=90°-∠B=90°-52°=38°.
点评 此题考查了平行线的性质与垂直的定义.注意两直线平行,内错角相等.注意掌握辅助线的作法是解此题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
13.一个数在数轴上的对应点与它的相反数在数轴上的对应点的距离是5个单位长度,那么这个数是( )
| A. | 5或-5 | B. | 5或-$\frac{5}{2}$ | C. | $\frac{5}{2}$或-$\frac{5}{2}$ | D. | -5或$\frac{5}{2}$ |
17.正方形具有而菱形不具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线相等 | ||
| C. | 对角线互相垂直且平分 | D. | 对角线互相垂直 |
 如图,已知四边形ABCD是平行四边形,若AF、BE分别是∠DAB、∠CBA的平分线,AB=4,BC=3,则EF的长是( )
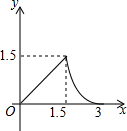
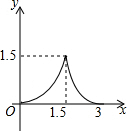
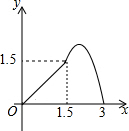
如图,已知四边形ABCD是平行四边形,若AF、BE分别是∠DAB、∠CBA的平分线,AB=4,BC=3,则EF的长是( )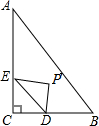 如图,∠C=90°,BC=3,AB=5,点D是BC上一动点,CD=x,DE∥AB交AC于点E,以直线DE为轴作△CDE的轴对称△PDE,△PDE落在△ABC内的面积为y,则下列能刻画y与x之间函数关系的图象是( )
如图,∠C=90°,BC=3,AB=5,点D是BC上一动点,CD=x,DE∥AB交AC于点E,以直线DE为轴作△CDE的轴对称△PDE,△PDE落在△ABC内的面积为y,则下列能刻画y与x之间函数关系的图象是( )