题目内容
20.A、B、C三名同学竞选学生会主席,他们的笔试和口试成绩(单位:分)分别用两种方式进行了统计,如表和图:| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 80 | 85 |
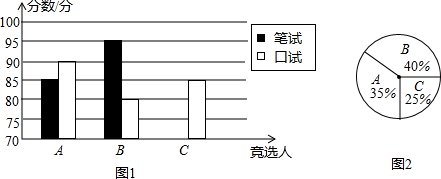
(1)请将表和图中的空缺部分补充完整;
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图(没有弃权票,每名学生只能推荐一个),请计算每人的得票数;
(3)若每票计1分,学校将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
分析 (1)根据条形统计图找出A的口试成绩,填写表格即可;找出C的笔试成绩,补全条形统计图即可;
(2)由300分别乘以扇形统计图中各学生的百分数即可得到各自的得分,再根据加权平均数的计算方法计算可得.(2)A的得票为300×35%=105(张),B的得票为300×40%=120(张),C的得票为:300×25%=75(张);
(3)分别通过加权平均数的计算方法计算A的成绩,B的成绩,C的成绩,综合三人的得分,则B应当选.
解答 解:(1)由条形统计图得:A同学的口试成绩为90;补充直方图,如图所示:
| A | B | C | |
| 笔试 | 85 | 95 | 90 |
| 口试 | 90 | 80 | 85 |
(3)∵$\overline{{x}_{A}}$=$\frac{85×3+90×4+105×3}{10}$=93,$\overline{{x}_{B}}$=$\frac{95×3+80×4+120×3}{10}$=96.5,$\overline{{x}_{C}}$=$\frac{90×3+85×4+75×3}{10}$=83.5,
∵$\overline{{x}_{B}}$>$\overline{{x}_{A}}$>$\overline{{x}_{C}}$,
∴B学生能当选.
点评 此题考查了条形统计图、扇形统计图及加权平均数的计算,能正确识别表格与统计图是解本题的关键.

练习册系列答案
相关题目
11. 一个不等式的解如图所示,则此不等式可能是( )
一个不等式的解如图所示,则此不等式可能是( )
 一个不等式的解如图所示,则此不等式可能是( )
一个不等式的解如图所示,则此不等式可能是( )| A. | $\frac{x+4}{x-2}$≤0 | B. | $\frac{x+2}{x-4}$≤0 | C. | $\frac{x-4}{x+2}$≤0 | D. | (x-4)(x+2)≤0 |
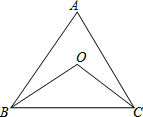 如图,点O是△ABC的∠ABC、∠ACB的平分线的交点,若∠A为锐角,∠BOC=α°,则α的取值范围为90°<α<135°.
如图,点O是△ABC的∠ABC、∠ACB的平分线的交点,若∠A为锐角,∠BOC=α°,则α的取值范围为90°<α<135°. 某学校要了解学生上学交通情况,选取九年级全体学生进行调查.根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°.已知九年级乘公交车上学的人数为50人.九年级学生中,骑自行车和乘公交车上学哪个更多?多多少人?
某学校要了解学生上学交通情况,选取九年级全体学生进行调查.根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°.已知九年级乘公交车上学的人数为50人.九年级学生中,骑自行车和乘公交车上学哪个更多?多多少人?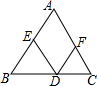 如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.
如图,△ABC中,D,E,F分别为三边BC,BA,AC上的点,∠B=∠DEB,∠C=∠DFC.若∠A=70°,求∠EDF的度数.