题目内容
6.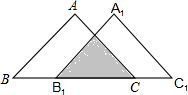 如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1.若B1C=3$\sqrt{2}$.△ABC与△A1B1C1重叠部分面积为$\frac{9}{2}$.
如图,将等腰直角△ABC沿BC方向平移得到△A1B1C1.若B1C=3$\sqrt{2}$.△ABC与△A1B1C1重叠部分面积为$\frac{9}{2}$.
分析 判断出重叠部分是等腰直角三角形,然后根据等腰直角三角形的面积公式列式计算即可得解.
解答 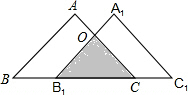 解:∵△ABC的等腰直角三角形,
解:∵△ABC的等腰直角三角形,
∴∠ACB=∠ABC=45°,
∴根据重叠部分是等腰直角三角形,
∴OB1=OC=$\frac{\sqrt{2}}{2}$×3$\sqrt{2}$=3
∴重叠部分的面积=$\frac{1}{2}$×3×3=$\frac{9}{2}$,
故答案为:$\frac{9}{2}$.
点评 本题考查了平移的性质,判断出阴影部分是等腰直角三角形是解题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D为BC上一点且与B、C不重合.∠ADE=45°,交AC于E.
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2,点D为BC上一点且与B、C不重合.∠ADE=45°,交AC于E.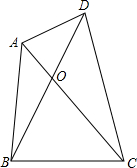 如图,S△AOD=3,S△AOB=4,S△COD=6,求S△BOC.
如图,S△AOD=3,S△AOB=4,S△COD=6,求S△BOC.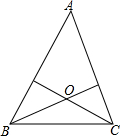 已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.
已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC,如图,若点O在△ABC的内部,求证:∠ABO=∠ACO.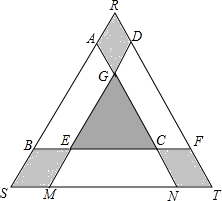 某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.
某学校矩形数学家“摇篮杯”会徽设计大赛,小明设计的会徽如图所示.正△DEF和正△GMN均由正△ABC平移得到,点A,B,M,N,F,D在正△RST边上,EC=2BE.若阴影部分的面积为$\frac{5\sqrt{3}}{32}$,则正△RST的边长是$\frac{5}{4}$.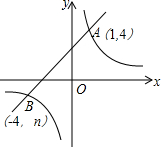 如图,反比例函数y=$\frac{k}{x}$(k≠0)的图象与一次函数y=x+b的图象交于A(1,4)、B(-4,n).
如图,反比例函数y=$\frac{k}{x}$(k≠0)的图象与一次函数y=x+b的图象交于A(1,4)、B(-4,n).