题目内容
12.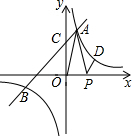 如图所示,直线y=2x+3与双曲线y=$\frac{m}{x}$相交于A,B两点,与轴交于点C,且△OCA的面积为1.5.
如图所示,直线y=2x+3与双曲线y=$\frac{m}{x}$相交于A,B两点,与轴交于点C,且△OCA的面积为1.5.(1)求双曲线y=$\frac{m}{x}$的解析式;
(2)若点D,B关于原点对称,一动点P沿着x轴运动,则|PA-PD|是否有最大值?如果有,请确定点P的位置;如果没有,请说明理由.
分析 (1)根据直线解析式求得C点坐标,然后根据三角形的面积求得A的横坐标,代入直线解析式即可求得A的坐标,代入反比例函数解析式即可求得m;
(2)联立解析式求得B的坐标,根据对称的性质求得D的坐标,因为当A、D、P在一条直线上时,|PA-PD|的值最大,所以根据待定系数法求得直线AD的解析式,然后即可求得直线与x轴的交点,即为P点.
解答 解:(1)由直线y=2x+3可知,C(0,3),
∴OC=3,
∵△OCA的面积为1.5.
∴$\frac{1}{2}$OC•xA=1.5,
∴xA=1,
代入y=2x+3得,y=2×1+3=5,
∴A(1,5),
把A代入y=$\frac{m}{x}$解得,m=5,
∴双曲线的解析式为y=$\frac{5}{x}$;
(2)解$\left\{\begin{array}{l}{y=\frac{5}{x}}\\{y=2x+3}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\frac{5}{2}}\\{{y}_{2}=-2}\end{array}\right.$,
∴B(-$\frac{5}{2}$,-2),
∵点D,B关于原点对称,
∴D($\frac{5}{2}$,2),
设直线AD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{k+b=5}\\{\frac{5}{2}k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=7}\end{array}\right.$,
∴直线AD的解析式为y=-2x+7,
令y=0,则-2x+7=0,解得x=$\frac{7}{2}$,
∴当P($\frac{7}{2}$,0)时,|PA-PD|有最大值.
点评 主要考查了反比例函数与一次函数的交点问题,待定系数法求反比例函数和一次函数的解析式,中心对称的性质,(2)确定出P点的位置是解题的关键.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案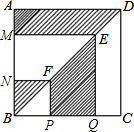 正方形ABCD的边长为2,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于2.
正方形ABCD的边长为2,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于2.
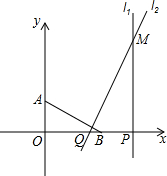 如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒
如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒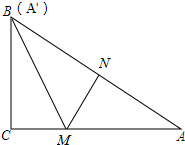 如图,在Rt△ABC中,∠ACB=90°,点M在边AC上,过点M作MN⊥AB与点N,将△MNA沿着MN折叠,恰好点A的对应点A′与点B重合.
如图,在Rt△ABC中,∠ACB=90°,点M在边AC上,过点M作MN⊥AB与点N,将△MNA沿着MN折叠,恰好点A的对应点A′与点B重合.