题目内容
2.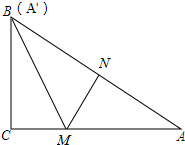 如图,在Rt△ABC中,∠ACB=90°,点M在边AC上,过点M作MN⊥AB与点N,将△MNA沿着MN折叠,恰好点A的对应点A′与点B重合.
如图,在Rt△ABC中,∠ACB=90°,点M在边AC上,过点M作MN⊥AB与点N,将△MNA沿着MN折叠,恰好点A的对应点A′与点B重合.(1)若∠A=30°,求证:CM=NM;
(2)若BC=1,AC=$\sqrt{2}$,求此时CM的长度.
分析 (1)由∠ACB=90°,∠A=30°可求得∠ABC=60°,然后由翻折的性质可知∠NBM=30°,从而可求得∠CBM=∠NBM=30°,最后由角平分线的性质可证明CM=NM;
(2)设CM=x,则MA=$\sqrt{2}-x$,由翻折的性质可知:MA=BM=$\sqrt{2}-x$,最后在Rt△BCM中由勾股定理可求得x的值.
解答 解:(1)∵∠ACB=90°,∠A=30°,
∴∠ABC=60°.
由翻折的性质可知:∠NBM=∠A=30°.
∴∠CBM=∠NBM=30°.
又∵MN⊥AB,BC⊥CA,
∴CM=NM.
(2)CM=x,则MA=$\sqrt{2}-x$.
由翻折的性质可知:MA=BM=$\sqrt{2}-x$.
在Rt△BCM中,由勾股定理可知:MB2=CM2+BC2,即$(\sqrt{2}-x)^{2}={x}^{2}+{1}^{2}$.
解得:x=$\frac{\sqrt{2}}{4}$.
故CM=$\frac{\sqrt{2}}{4}$.
点评 本题主要考查的是翻折的性质、勾股定理的应用、利用勾股定理列出关于x的方程是解题的关键.

练习册系列答案
相关题目
10.已知:四边形ABCD是正方形,在平面内找一点P满足△PAB,△PBC,△PCD,△PAD均为等腰三角形,这样的点P有( )个.
| A. | 7个 | B. | 8个 | C. | 9个 | D. | 10个 |
17.下列各组数中,互为相反数的是( )
| A. | 3与$\frac{1}{3}$ | B. | (-1)2与1 | C. | -14与(-1)2 | D. | 2与|-2| |
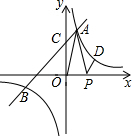 如图所示,直线y=2x+3与双曲线y=$\frac{m}{x}$相交于A,B两点,与轴交于点C,且△OCA的面积为1.5.
如图所示,直线y=2x+3与双曲线y=$\frac{m}{x}$相交于A,B两点,与轴交于点C,且△OCA的面积为1.5. 已知AB是直径,∠C等于15度,∠BAD的度数=75°.
已知AB是直径,∠C等于15度,∠BAD的度数=75°.
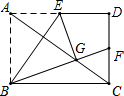 如图,在矩形ABCD中,点E为AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形ABCD的对角线AC上,延长BG交CD于F,连接EF.求$\frac{BE}{EF}$的值.
如图,在矩形ABCD中,点E为AD的中点,将△ABE沿BE折叠后得到△GBE,点G恰好在矩形ABCD的对角线AC上,延长BG交CD于F,连接EF.求$\frac{BE}{EF}$的值.