题目内容
2.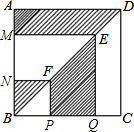 正方形ABCD的边长为2,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于2.
正方形ABCD的边长为2,点E、F分别是对角线BD上的两点,过点E、F分别作AD、AB的平行线,如图所示,则图中阴影部分的面积之和等于2.
分析 证明图中的阴影部分与对应的非阴影部分全等,则图中阴影部分的面积是正方形的面积的一半即可解决问题.
解答 解:如图,
∵FP∥CD,
∴∠BPF=∠C=90°(同位角相等);
在△BFP和△BDC中,
$\left\{\begin{array}{l}{∠FBP=∠DBC}\\{∠BPF=∠C}\end{array}\right.$,
∴△BFP∽△BDC(AA),
∴$\frac{FP}{CD}$=$\frac{BF}{BD}$,
同理,得$\frac{NF}{AD}$=$\frac{BF}{BD}$,
又∵AD=CD,
∴NF=FP,
∵∠BNF=∠BPF=90°,BF=BF,
∴△BNF≌△BPF,
∴S△BNF=S△BPF,
同理,求得多边形NFEM与多边形PFEQ的面积相等,多边形MEDA与多边形QEDC的面积相等,
∴图中阴影部分的面积是正方形ABCD面积的一半,$\frac{1}{2}$×2×2=2.
故答案为:2.
点评 此题考查了轴对称的性质,解答本题时主要运用了正方形的性质,相似三角形的判定以及相似三角形的性质.所以,在以后的解题中合理的利用已学的定理与性质会降低题的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.一个不透明的袋子中有2个白球,1个黄球和1个红球,这些球除颜色不同外其他完全相同,若从袋子中随机摸出1个球后,放回摇匀,再取出1个球,则两次取出都是白球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
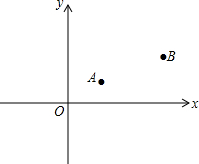 如图,已知A、B两村庄的坐标分别为A(2,2),B(7,4),一辆汽车在x轴上行驶,从原点O出发.
如图,已知A、B两村庄的坐标分别为A(2,2),B(7,4),一辆汽车在x轴上行驶,从原点O出发. 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是SSS(填SSS,SAS,AAS,ASA中的一种).
用直尺和圆规作一个角等于已知角的示意图如图所示,则说明∠A′O′B′=∠AOB的依据是SSS(填SSS,SAS,AAS,ASA中的一种).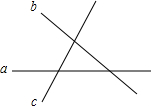 如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有4处.
如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有4处.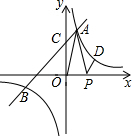 如图所示,直线y=2x+3与双曲线y=$\frac{m}{x}$相交于A,B两点,与轴交于点C,且△OCA的面积为1.5.
如图所示,直线y=2x+3与双曲线y=$\frac{m}{x}$相交于A,B两点,与轴交于点C,且△OCA的面积为1.5.