题目内容
4．计算（1）$\sqrt{25}$+$\root{3}{-8}$-（π-1）0；
（2）a3•a8•a+（a2）6+（-2a4）3
（3）（6a2b-9a3）÷（-3a）2；
（4）（2a+3）2-（a-1）•（4a+9）
分析 （1）根据算术平方根、立方根、零指数幂进行计算即可；
（2）根据同底数幂的乘法、幂的乘方和积的乘方进行计算即可；
（3）根据多项式除以单项式的法则进行计算即可；
（4）根据完全平方公式和多项式乘以多项式进行计算即可．
解答 解：（1）原式=5-2-1
=2；
（2）原式=a12+a12+（-8a12）
=-6a12；
（3）原式=6a2b÷9a2-9a3÷9a2；
=$\frac{2}{3}$b-a；
（4）原式=4a2+12a+9-4a2-5a+9
=7a+18．
点评 本题考查了整式的混合运算，实数的运算以及零指数幂运算，掌握运算法则是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．
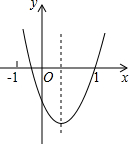已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论正确的个数是（ ）
①a-b+c＞0②方程ax2+bx+c=0两根都大于零③y随x的增大而增大④一次函数y=x+bc的图象不过第二象限．
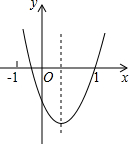已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论正确的个数是（ ）①a-b+c＞0②方程ax2+bx+c=0两根都大于零③y随x的增大而增大④一次函数y=x+bc的图象不过第二象限．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
12．2016年4月6日22：20某市某个观察站测得：空气中PM2.5含量为每立方米23μg，1g=1000000μg，则将23μg用科学记数法表示为（ ）
| A． | 2.3×10-7g | B． | 23×10-6g | C． | 2.3×10-5g | D． | 2.3×10-4g |
19．
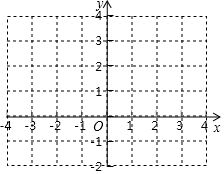探索研究：通过对一次函数、反比例函数的学习．我们积累了一定的经验．下面我们借鉴以往研究函数的经验，探索y=$\frac{1}{|x|}$的图象和性质．
（1）在平面直角坐标系中，画出函数y=$\frac{1}{|x|}$的图象．
①列表填空：
②描点、连线，画出y=$\frac{1}{|x|}$的图象；
（2）结合所画函数图象，写出y=$\frac{1}{|x|}$两条不同类型的性质；
①当x＜0时，y随x的增大而增大；②当x＞0时，y随x的增大而减小．
知识运用：观察你所画的函数图象，解答下列问题：
（3）若点A（a，c），B（b，c）为该函数图象上不同的两点，则a+b=0．
（4）不等式$\frac{1}{|x|}$＞2的解集是-$\frac{1}{2}$＜x＜0或0＜x＜$\frac{1}{2}$．．
探索研究：通过对一次函数、反比例函数的学习．我们积累了一定的经验．下面我们借鉴以往研究函数的经验，探索y=$\frac{1}{|x|}$的图象和性质．（1）在平面直角坐标系中，画出函数y=$\frac{1}{|x|}$的图象．
①列表填空：
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 2 | 1 | $\frac{1}{2}$ | $\frac{1}{3}$ |
（2）结合所画函数图象，写出y=$\frac{1}{|x|}$两条不同类型的性质；
①当x＜0时，y随x的增大而增大；②当x＞0时，y随x的增大而减小．
知识运用：观察你所画的函数图象，解答下列问题：
（3）若点A（a，c），B（b，c）为该函数图象上不同的两点，则a+b=0．
（4）不等式$\frac{1}{|x|}$＞2的解集是-$\frac{1}{2}$＜x＜0或0＜x＜$\frac{1}{2}$．．
9．全世界人民踊跃为四川汶川灾区人民捐款，到6月3日止各地共捐款约424亿元，用科学记数法表示约为（ ）元．（保留两个有效数字）
| A． | 4.23×1010 | B． | 4.24×1010 | C． | 4.24×1011 | D． | 4.23×1011 |