题目内容
18.观察下面的变形规律:$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}-1$,$\frac{1}{\sqrt{3}+\sqrt{2}}$=$\sqrt{3}-\sqrt{2}$,$\frac{1}{\sqrt{4}+\sqrt{3}}$=$\sqrt{4}-\sqrt{3}$,$\frac{1}{\sqrt{5}+\sqrt{4}}$=$\sqrt{5}-\sqrt{4}$,…
解答下面的问题:
(1)若n为正整数,请你猜想$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
(2)计算:
($\frac{1}{\sqrt{2}+1}+\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2016}+\sqrt{2015}}$)×($\sqrt{2016}+1$)
分析 (1)根据题意确定出一般性规律,写出即可;
(2)原式分母有理化后,计算即可得到结果.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(2)原式=[($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+($\sqrt{4}$-$\sqrt{3}$)+…+($\sqrt{2016}$-$\sqrt{2015}$)]($\sqrt{2016}$+1)
=($\sqrt{2016}$-1)($\sqrt{2016}$+1)
=($\sqrt{2016}$)2-12
=2016-1
=2015.
点评 此题考查了分母有理化,弄清题中分母有理化规律是解本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
9.一个多边形的内角和是外角和的n倍(n是正整数),则该多边形的边数是( )
| A. | 2n+2 | B. | n+1 | C. | 2n+1 | D. | 2n+4 |
6.如果一个三角形的一条边是另一条边的2倍,并且有一个角是30°,那么这个三角形的形状是( )
| A. | 直角三角形 | B. | 钝角三角形 | C. | 锐角三角形 | D. | 不能唯一确定 |
7.|-9|的值是( )
| A. | 9 | B. | -9 | C. | $\frac{1}{9}$ | D. | -$\frac{1}{9}$ |
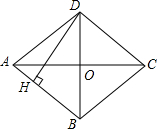 如图,四边形ABCD是菱形,对角线AC=8cm,BD=6 cm,DH⊥AB于H,DH的长是$\frac{24}{5}$cm.
如图,四边形ABCD是菱形,对角线AC=8cm,BD=6 cm,DH⊥AB于H,DH的长是$\frac{24}{5}$cm. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E.若AC=6,BC=8,CD=3.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E.若AC=6,BC=8,CD=3.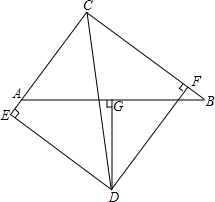 已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.
已知:如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB边的垂直平分线相交于点D,DE⊥AC,DF⊥BC,垂足分别是E、F.