题目内容
1.已知有理数x、y、z满足关系式(x-4)2+$\frac{1}{4}$|x+y-z|=0,则(5x+3y-3z)2003的末位数字是多少?分析 由非负数的性质得x-4=0,x+y-z=0再代入求得5x+3y-3z的值,得出(5x+3y-3z)2003的末位数字.
解答 解:∵(x-4)2+$\frac{1}{4}$|x+y-z|=0,
∴x-4=0,x+y-z=0,
∴x=4,y-z=-4,
∴5x+3y-3z=5×4+3×(-4)=8,
∵81=8,82=64,83=512,84=4096,85=32768…,
末位数字是8、4、2、6、8、4、2、6、8、…依次循环,
2003÷4=500…3,
∴820103的末尾数字为2,即(5x+3y-3z)2003的末位数字是2.
点评 本题考查了尾数特征,非负数的性质,根据几个非负数的和为0时,这几个非负数都为0求出x=4,y-z=-4是解题的关键.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
9.若一元二次方程x2+ax+b=0的两根为整数,且两根的平方和为2009,则这种方程有( )
| A. | 1个 | B. | 2个 | C. | 4个 | D. | 8个 |
11.为了保护生态平衡,绿化环境,国家大力鼓励“退耕还林、还草”,其补偿政策如表(一);某农户承包了一片山坡地种树种草,所得到国家的补偿如表(二).问:该农户种树、种草各多少亩?
表(一)种树、种草每亩每年补粮补钱情况表
表(二)该农户收到乡政府下发的当种树种草亩数及年补偿通知单
表(一)种树、种草每亩每年补粮补钱情况表
| 种树 | 种草 | |
| 补粮 | 150千克 | 100千克 |
| 补钱 | 200元 | 150元 |
| 种树、种草 | 补粮 | 补钱 |
| 30亩 | 4000千克 | 5500元 |
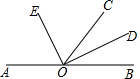 如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC
如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC 如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①ab>0;②a-b>0;③a+b>0;④|a|-|b|>0中正确的有( )
如图,数轴上A、B两点分别对应有理数a、b,则下列结论:①ab>0;②a-b>0;③a+b>0;④|a|-|b|>0中正确的有( )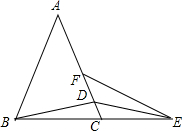 如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.
如图,△ABC中,AB=AC,点D在AC上,点E在BC的延长线上,DB=DE,∠AFE+∠A=180°.求证:EF=AD.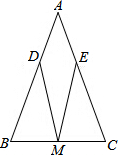 如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE,
如图,已知:△ABC中,AB=AC,M是BC的中点,D、E分别是AB、AC边上的点,且BD=CE,