题目内容
1.已知点(3,-2)在反比例函数y=$\frac{k}{x}$的图象上,则下列点也在该反比例函数y=$\frac{k}{x}$的图象的是( )| A. | (3,-3) | B. | (-2,3) | C. | (1,6) | D. | (-2,-3) |
分析 先根据反比例函数y=$\frac{k}{x}$图象过点(3,-2)求出k的值,再根据k=xy的特点进行解答即可.
解答 解:∵反比例函数y=$\frac{k}{x}$图象过点(3,-2),
∴-2=$\frac{k}{3}$,即k=-6,
A、∵3×(-3)=-9≠-6,∴此点不在反比例函数的图象上,故本选项错误;
B、∵-2×3=-6,∴此点在反比例函数的图象上,故本选项正确;
C、∵1×6=6≠-6,∴此点不在反比例函数的图象上,故本选项错误;
D、∵-2×(-3)=6≠-6,∴此点不在反比例函数的图象上,故本选项错误.
故选:B.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
13.顺次连接下面四边形各边中点,得到的四边形一定是正方形的是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
11.某商场新近一批A、B两种型号的节能防近视台灯,每台进价分别为200元、170元,近两周的销售情况如下:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的台灯的销售单价;
(2)若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
(3)在(2)的条件下,该商场销售完这30台台灯能否实现利润为1400元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第二周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的台灯的销售单价;
(2)若该商场准备用不多于5400元的金额再购进这两种型号的台灯共30台,求A种型号的台灯最多能购进多少台?
(3)在(2)的条件下,该商场销售完这30台台灯能否实现利润为1400元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
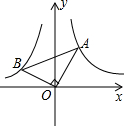 如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.