题目内容
8.(1)解方程:$\frac{2}{3x-1}$-1=$\frac{3}{6x-2}$;(2)解不等式组:$\left\{\begin{array}{l}{4x-3>x}\\{x+4<2x-1}\end{array}\right.$.
分析 (1)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)去分母得:4-6x+2=3,
解得:x=$\frac{1}{2}$,
经检验x=$\frac{1}{2}$是分式方程的解;
(2)$\left\{\begin{array}{l}{4x-3>x①}\\{x+4<2x-1②}\end{array}\right.$,
由①得:x>1,
由②得:x>5,
故不等式组的解集为x>5.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
18.在平面直角坐标系中,点M(-2,1)关于x轴对称的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.顺次连接下面四边形各边中点,得到的四边形一定是正方形的是( )
| A. | 正方形 | B. | 菱形 | C. | 矩形 | D. | 平行四边形 |
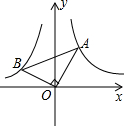 如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{1}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{1}{3}$.