��Ŀ����
6����ͼ1��������y=-x2-4x+5��x�ύ�ڵ�A��B���㣬��y�ύ�ڵ�C����DΪ�����ߵĶ��㣮��1����ֱ��AC�Ľ���ʽ������D�����ꣻ
��2������CD����P��ֱ��AC�Ϸ���������һ���㣨�����A��C�غϣ�����P��PE��x�ύֱ��AC�ڵ�E����PF��CD��ֱ��AC�ڵ�F�����߶�PE+PFȡ���ֵʱ���������߶Գ�������һ��L����y������һ��K������OL��LK��PK�����߶�OL+LK+PK����Сֵ���������ʱ��L�����꣮
��3����ͼ2����M��-2��-1��Ϊ�����߶Գ�����һ�㣬��N��2��7��Ϊֱ��AC��һ�㣬��GΪֱ��AC�������߶Գ���Ľ��㣬����MN��AM����H���߶�MN�ϵ�һ�����㣬����GH������MGH��GH���۵õ���M��GH����M�ĶԳƵ�ΪM�䣩�����Ƿ���ڵ�H��ʹ�á�M��GH���NGH�غϲ��ֵ�ͼ��Ϊֱ�������Σ������ڣ������NH�ij����������ڣ���˵�����ɣ�

���� ��1���ֱ���x=0��y=0�����A��B��C�������꣬��ֱ��AC����ʽΪy=kx+b��A��C�����������ⷽ���鼴�ɣ�
��2����ͼ1�У�����PC��PA����PT��AC��T������PT���ʱ��PE��PF���PE+PF���ʱ��PAC����������P��m��-m2-4m+5�����������κ���ȷ����PAC������ʱ��P���꣬����O���ڶԳ���ĶԳƵ�O�䣬O�����y��ĶԳƵ�O�壬����PO�彻y����K������O��K���Գ�����L����ʱOL+LK+PK��̣��ֱ����ֱ��PO�壬O��K�Ľ���ʽ���ɽ�����⣮
��3�����ڣ��������������ۢ���ͼ2�У��ص������ǡ�GHT������GHT=90��ʱ������ͼ3�У��ص������ǡ�GHT������GTH=90��ʱ����HE��GM��E������ͼ4�У��ص������ǡ�GHT������GTH=90��ʱ����GF��MN��F��
��� �⣺��1����y=0����-x2-4x+5=0�����x=-5��1��
��A��-5��0����B��1��0����
��x=0����y=5��
��C��0��5����
��ֱ��AC����ʽΪy=kx+b������$\left\{\begin{array}{l}{b=5}\\{-5k+b=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=1}\\{b=5}\end{array}\right.$��
��ֱ��AC����ʽΪy=x+5��
��y=-x2-4x+5=-��x+2��2+9��
�ඥ��D���꣨-2��9����
��2��������һ����ͼ1�У�����PC��PA����PT��AC��T��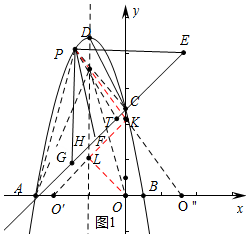
�ߵ�P���˶������У���PEF����PFE�Dz���ģ�
�൱��PT���ʱ��PE��PF���PE+PF���ʱ��PAC����������P��m��-m2-4m+5����
��S��PAC=S��PAO+S��PCO-S��AOC=$\frac{1}{2}$��5����-m2-4m+5��+$\frac{1}{2}$��5����-m��-$\frac{1}{2}$��5��5=-$\frac{5}{2}$m2-$\frac{25}{2}$m=-$\frac{5}{2}$��m+$\frac{5}{2}$��2+$\frac{125}{8}$��
��-$\frac{5}{2}$��0��
��m=-$\frac{5}{2}$ʱ����PAC������ʱP��-$\frac{5}{2}$��$\frac{35}{4}$����
����������Գ��ύAC��H����PG��y�ύAC��G��
��A��-5��0����C��0��5����
��ֱ��AC�Ľ���ʽΪy=x+5��
��P��m��-m2-4m+5������G��m��m+5������֪PG=PE=-m2-4m+5-m-5=-m2-5m��
��CD=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��DH=6��
�ɡ�PFG�ס�DCH����$\frac{PF}{CD}$=$\frac{PG}{DH}$����$\frac{PF}{2\sqrt{5}}$=$\frac{-{m}^{2}-5m}{6}$��
��PF=-$\frac{\sqrt{5}}{3}$m2-$\frac{5\sqrt{5}}{3}$m��
��PE+PF=-��1+$\frac{\sqrt{5}}{3}$��m2-��5+$\frac{5\sqrt{5}}{3}$��m��
��-��1+$\frac{\sqrt{5}}{3}$����0��
��m=-$\frac{5+\frac{5\sqrt{5}}{3}}{2��1+\frac{\sqrt{5}}{3}��}$=-$\frac{5}{2}$ʱ��PE+PF��ֵ���ʱP��-$\frac{5}{2}$��$\frac{35}{4}$����
����O���ڶԳ���ĶԳƵ�O�䣬O�����y��ĶԳƵ�O�壬����PO�彻y����K������O��K���Գ�����L����ʱOL+LK+PK��̣�
���ɣ���LO=LO�䣬KO��=KO�壬
��LO+LK+PK=��LO��+KL��+PL=KO��+PK=KO��+PK=PO�壬
��LO+LK+PK��̣�������֮���߶���̣�����ʱ��Сֵ=$\sqrt{��4+\frac{5}{2}��^{2}+��\frac{35}{4}��^{2}}$=$\frac{\sqrt{1901}}{4}$��
��O�壨4��0����
��ɵ�ֱ��PO��Ľ���ʽΪy=-$\frac{35}{26}$x+$\frac{70}{13}$��
���K���꣨0��$\frac{70}{13}$������O�䣨-4��0����
��ֱ��O��K����ʽΪ��y=$\frac{35}{26}$x+$\frac{70}{13}$��
��x=-2ʱ��y=$\frac{35}{13}$��
���L���꣨-2��$\frac{35}{13}$����
��3�����ڣ�
����ͼ2�У��ص������ǡ�GHT������GHT=90��ʱ��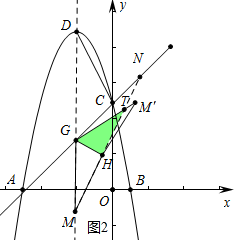
��M��-2��-1����N��2��7����
��ɵ�ֱ��MN�Ľ���ʽΪy=2x+3��
��G��-2��3����GH��MN��
��ɵ�ֱ��GH�Ľ���ʽΪy=-$\frac{1}{2}$x+2��
��$\left\{\begin{array}{l}{y=2x+3}\\{y=-\frac{1}{2}x+2}\end{array}\right.$���$\left\{\begin{array}{l}{x=-\frac{2}{5}}\\{y=\frac{11}{5}}\end{array}\right.$��
���H���꣨-$\frac{2}{5}$��$\frac{11}{5}$����
��NH=$\sqrt{��2+\frac{2}{5}��^{2}+��7-\frac{11}{5}��^{2}}$=$\frac{12\sqrt{5}}{5}$��
����ͼ3�У��ص������ǡ�GHT������GTH=90��ʱ����HE��GM��E��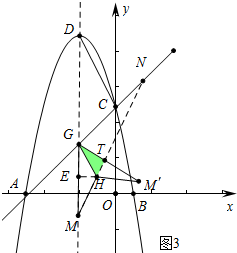
�ߡ�HGT=��HGE��HT��GT��HE��GE��
��HT=HE����HT=HE=x��
�ɢٿ�֪��GT=GE=$\sqrt{��-2+\frac{2}{3}��^{2}+��3-\frac{5}{3}��^{2}}$=$\frac{4}{3}$$\sqrt{2}$��TM=$\frac{4}{3}$$\sqrt{5}$��MN=4$\sqrt{5}$��
�ɡ�MEH�ס�MTG���õ���$\frac{ME}{MT}$=$\frac{MH}{GM}$��
��$\frac{4-\frac{4}{3}\sqrt{2}}{\frac{4}{3}\sqrt{5}}$=$\frac{MH}{4}$��
��MH=$\frac{12\sqrt{5}}{5}$-$\frac{4}{5}$$\sqrt{10}$��
��HN=MN-MH=$\frac{8}{5}$$\sqrt{5}$+$\frac{4}{5}$$\sqrt{10}$��
����ͼ4�У��ص������ǡ�GHT������GTH=90��ʱ����GF��MN��F��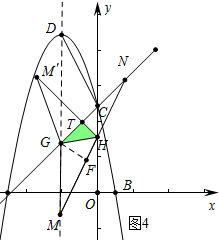
�ɢڿ�֪��GF=GT=$\frac{4}{3}$$\sqrt{2}$��FN=$\frac{8}{3}$$\sqrt{5}$��GN=4$\sqrt{2}$��
�ɡ�NTH�ס�NFG��$\frac{NH}{NG}$=$\frac{TN}{NF}$��
��$\frac{NH}{4\sqrt{2}}$=$\frac{4\sqrt{2}-\frac{4}{3}\sqrt{2}}{\frac{8}{3}\sqrt{5}}$��
��NH=$\frac{8}{5}$$\sqrt{5}$��
���� ���⿼����κ����ۺ��⡢һ�κ�������ֵ���⡢���۱任��ֱ�������ε����ʡ����ɶ��������������ε����ʺ��ж���֪ʶ������Ĺؼ���������ô���ϵ����ȷ����������ʽ��ѧ��������ۣ�ѧ�ṹ�����κ���ȷ����ֵ���⣬ѧ�����öԳ�ȷ����Сֵ���⣬�����п�ѹ���⣮

| A�� | y���=-4 | B�� | y��С=-4 | C�� | y���=-3 | D�� | y��С=-3 |
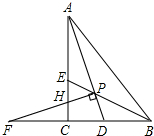
 ��ͼ����Rt��ABC�У���C=90�㣬M��AB���е㣬ME��AB��AC�ڵ�D����BC���ӳ����ڵ�E����֤��CM2=MD•ME��
��ͼ����Rt��ABC�У���C=90�㣬M��AB���е㣬ME��AB��AC�ڵ�D����BC���ӳ����ڵ�E����֤��CM2=MD•ME��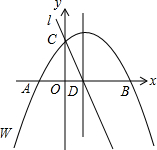 ��ͼ����ƽ��ֱ������ϵ�У�������w�ı���ʽΪy=-$\frac{4}{21}{x^2}+\frac{16}{21}x+4$��������w��X�ύ��A��B���㣨B��A�Ҳࣩ��y�ύ�ڵ�C�����ĶԳ�����x�ύ�ڵ�D��ֱ��L����C��D���㣮
��ͼ����ƽ��ֱ������ϵ�У�������w�ı���ʽΪy=-$\frac{4}{21}{x^2}+\frac{16}{21}x+4$��������w��X�ύ��A��B���㣨B��A�Ҳࣩ��y�ύ�ڵ�C�����ĶԳ�����x�ύ�ڵ�D��ֱ��L����C��D���㣮