题目内容
1.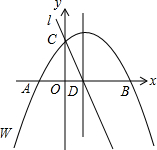 如图,在平面直角坐标系中,抛物线w的表达式为y=-$\frac{4}{21}{x^2}+\frac{16}{21}x+4$,抛物线w与X轴交于A、B两点(B在A右侧)与y轴交于点C,它的对称轴与x轴交于点D,直线L经过C、D两点.
如图,在平面直角坐标系中,抛物线w的表达式为y=-$\frac{4}{21}{x^2}+\frac{16}{21}x+4$,抛物线w与X轴交于A、B两点(B在A右侧)与y轴交于点C,它的对称轴与x轴交于点D,直线L经过C、D两点.(1)求A、B两点的坐标及直线L的函数表达式;
(2)将抛物线W沿x轴向右平移得到抛物线W′,设抛物线W′的对称轴与直线L交于点F,当△ACF是直角三角形时,求点F的坐标,并直接写出抛物线W′的函数表达式.
分析 (1)根据自变量与函数值对应关系,当函数值为零时,可得A、B点坐标,当自变量为零时,可得C点坐标,根据对称轴公式,可得D点坐标,根据待定系数法,可得l的解析式;
(2)根据余角性质,可得∠1与∠3的关系,根据正切的定义,可得关于F点的横坐标的方程,根据解方程,可得F点坐标,平移后的对称轴,根据平移后的对称轴,可得平移后的函数解析式.
解答  解:(1)当y=0时,-$\frac{4}{21}$x2+$\frac{16}{21}$x+4=0,
解:(1)当y=0时,-$\frac{4}{21}$x2+$\frac{16}{21}$x+4=0,
解得x1=-3,x2=7,
∴点A坐标为(-3,0),点B的坐标为(7,0).
∵-$\frac{b}{2a}$=2,
∴抛物线w的对称轴为直线x=2,
∴点D坐标为(2,0).
当x=0时,y=4,
∴点C的坐标为(0,4).
设直线l的表达式为y=kx+b,$\left\{\begin{array}{l}{b=4}\\{2k+b=0}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{k=-2}\\{b=4}\end{array}\right.$,
∴直线l的解析式为y=-2x+4;
(2)∵抛物线w向右平移,只有一种情况符合要求,
即∠FAC=90°,如图.
此时抛物线w′的对称轴与x轴的交点为G,
∵∠1+∠2=90°∠2+∠3=90°,
∴∠1=∠3,
∴tan∠1=tan∠3,
∴$\frac{FG}{AG}$=$\frac{AO}{CO}$.
设点F的坐标为(xF,-2xF+4),
∴$\frac{-(-2{x}_{F}+4)}{{x}_{F}-(-3)}$=$\frac{3}{4}$,
解得xF=5,-2xF+4=-6,
∴点F的坐标为(5,-6),
此时抛物线w′的函数表达式为y=-$\frac{4}{21}$x2+$\frac{40}{21}$x;
点评 本题考查了抛物线与x轴的交点问题,(1)利用了自变量与函数值的对应关系,待定系数法求函数解析式;(2)利用了余角的性质,正切函数的性质,利用等角的正切函数值相等得出关于F点横坐标的方程是解题关键

 阅读快车系列答案
阅读快车系列答案
| A. | $\frac{5}{2}$ | B. | $\frac{24}{5}$ | C. | $\frac{12}{5}$ | D. | 2 |
第18位也就是最后一位是数字校验码,是根据前面十七位数字码,按一定规则计算出来的校验码.算法如下:
规定第1-17位对应的系数分别为:7,9,10,5,8,4,2,1,6,3,7,9,10,5,8,4,2.将身份证号码的前17位数字分别乘以对应的系数,再把积相加.相加的结果除以11,求出余数.余数只可能有0,1,2,3,4,5,6,7,8,9,10这11种情况.其分别对应身份证号码的第18位数字如表所示.
| 余数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 第18位 | 1 | 0 | x | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 |
 在全民读书月活动中,某校随机调查了40名同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题,直接写出结果.
在全民读书月活动中,某校随机调查了40名同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题,直接写出结果.
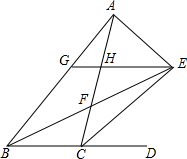 如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论:
如图,△ABC的内角∠ABC和外角∠ACD的平分线相交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论: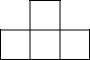 某几何体由若干个大小相同的正方体搭建而成,其主(正)视图、左(侧)视图相同,如图所示,则构成这个几何体至少需要几个正方体( )
某几何体由若干个大小相同的正方体搭建而成,其主(正)视图、左(侧)视图相同,如图所示,则构成这个几何体至少需要几个正方体( )