题目内容
 如图所示,在直角坐标系中,直线AB:y=-
如图所示,在直角坐标系中,直线AB:y=-| 4 |
| 3 |
考点:全等三角形的判定与性质,一次函数图象上点的坐标特征,正方形的性质
专题:
分析:如图,过点D作DF⊥y轴于点F,构建全等三角形△ADF≌△BAO,则由该全等三角形的性质得到DF=AO=4,AF=OB=3,故OF=1.易求D(-4,1).
解答: 解:如图,过点D作DF⊥y轴于点F.
解:如图,过点D作DF⊥y轴于点F.
∵直线AB:y=-
x+4交坐标轴于A、B两点,
∴当x=0时,y=4.
当y=0时,x=3,
即A(0,4),B(3,0).
∴OA=4,OB=3.
∵四边形ABCD是正方形,
∴AD=BA,∠DAB=90°,
∴∠ADF=∠BAO(等角的余角相等).
在△ADF与△BAO中,
,
∴△ADF≌△BAO(AAS),
∴DF=AO=4,AF=OB=3,故OF=1,
∴D(-4,1).
故答案是:(-4,1).
 解:如图,过点D作DF⊥y轴于点F.
解:如图,过点D作DF⊥y轴于点F.∵直线AB:y=-
| 4 |
| 3 |
∴当x=0时,y=4.
当y=0时,x=3,
即A(0,4),B(3,0).
∴OA=4,OB=3.
∵四边形ABCD是正方形,
∴AD=BA,∠DAB=90°,
∴∠ADF=∠BAO(等角的余角相等).
在△ADF与△BAO中,
|
∴△ADF≌△BAO(AAS),
∴DF=AO=4,AF=OB=3,故OF=1,
∴D(-4,1).
故答案是:(-4,1).
点评:本题考查了正方形的性质、一次函数图象上点的坐标特征以及全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 实数a,b在数轴上对应点A,B的位置如图所示,且|a|=2,|b|是16的一个平方根.求代数式|a+b|-
实数a,b在数轴上对应点A,B的位置如图所示,且|a|=2,|b|是16的一个平方根.求代数式|a+b|-
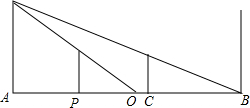 小静晚上从路灯A走向电线杆B,当她走到点P时,发现她影子的顶部刚好接触到路灯A与电线杆B的中点O处;当她再向前走12m到达C点时,发现她影子的顶部刚好接触到电线杆B的底部,已知小静身高1.60m,路灯高4.8m,求路灯A与电线杆B之间的距离.
小静晚上从路灯A走向电线杆B,当她走到点P时,发现她影子的顶部刚好接触到路灯A与电线杆B的中点O处;当她再向前走12m到达C点时,发现她影子的顶部刚好接触到电线杆B的底部,已知小静身高1.60m,路灯高4.8m,求路灯A与电线杆B之间的距离.