题目内容
6.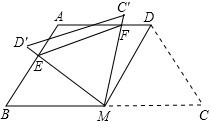 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.将△MDC绕点M旋转,旋转后对应的三角形为△MC′D′,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,连接EF,求证:EF∥C′D′.
如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中点.将△MDC绕点M旋转,旋转后对应的三角形为△MC′D′,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点F时,连接EF,求证:EF∥C′D′.
分析 连接BD,AM,首先证明出∠ABD=∠DBC,结合题干条件得到∠BDC=90°,进而得到DC=MD,即可得到△MDC是等边三角形,四边形ABMD是菱形,△MAB,△MAD和△MC′D′是等边三角形,根据ASA证明△BME≌△AMF,于是得到ME=MF,结合∠EMF=60°,即可证明△MEF是等边三角形,可得∠EFM=∠C′=60°,则得EF∥C′D′.
解答 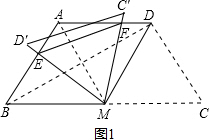 解:(1)连接BD,AM,
解:(1)连接BD,AM,
∵AD=AB,
∴∠ADB=∠ABD,
又∵AD∥BC,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵在等腰梯形ABCD中,∠ABC=∠C=60°,
∴∠ABD=∠DBC=30°,
∴∠BDC=90°,
∵M是BC的中点,
∴DM=BM=MC,
∴△MDC是等边三角形,
∴CD=DM=CM=BM=AD=AB,
∴四边形ABMD是菱形,
△MAB,△MAD和△MC′D′是等边三角形,
∠BMA=∠BME+∠AME=60°,∠EMF=∠AMF+∠AME=60°,
∴∠BME=∠AMF,
在△BME与△AMF中,
$\left\{\begin{array}{l}{∠ABC=∠FAM}\\{BM=AM}\\{∠BME=∠AMF}\end{array}\right.$,
∴△BME≌△AMF(ASA),
∴ME=MF,
∵∠EMF=∠DMC=60°,
∴△EMF是等边三角形,
∴∠FEM=∠EFM=60°,
∴∠EFM=∠C′=60°,
∴EF∥C′D′.
点评 本题主要考查了几何变换的综合题,此题涉及到等边三角形的性质和判定,旋转的性质,全等三角形的性质和判定,等腰梯形的性质等知识点,综合运用这些性质进行推理是解此题的关键.

练习册系列答案
相关题目
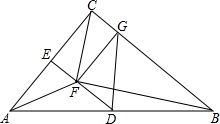 在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,点F是DE上一点,∠CBF=∠CAF,作FG⊥BC于点G,求证:
在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,点F是DE上一点,∠CBF=∠CAF,作FG⊥BC于点G,求证: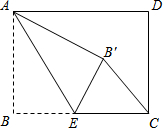 如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=4,点E是BC边上一点,连接AE,△ABE沿AE折叠,使点B落到点B′处,连接B′C,若B′C∥AE,则B′C的值为2.
如图,在矩形ABCD中,AB=2$\sqrt{3}$,BC=4,点E是BC边上一点,连接AE,△ABE沿AE折叠,使点B落到点B′处,连接B′C,若B′C∥AE,则B′C的值为2.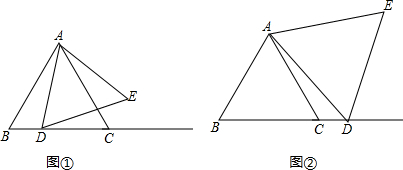
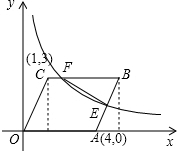 在直角坐标系中A点坐标为(4,0),C点坐标为(1,3)
在直角坐标系中A点坐标为(4,0),C点坐标为(1,3)