题目内容
11．已知∠1与∠2是同位角，则（ ）| A． | ∠1=∠2 | B． | ∠1＞∠2 | C． | ∠1＜∠2 | D． | 以上都有可能 |
分析 根据同位角的定义和平行线的性质判断即可．
解答 解：∵只有两直线平行时，同位角才可能相等，
∴根据已知∠1与∠2是同位角可以得出∠1=∠2或∠1＞∠2或∠1＜∠2，
三种情况都有可能，
故选D．
点评 本题考查了同位角和平行线的性质，能理解同位角的定义是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
1．某工厂承接了一批纸箱加工任务，用如图1所示的长方形和正方形纸板（长方形的宽与正方形的边长相等）加工成如图所示的竖式与横式两种无盖的长方形纸箱．（加工时接缝材料不计）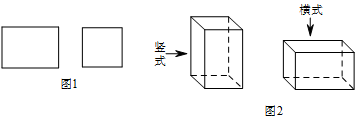
（1）若该厂购进正方形纸板1000张，长方形纸板2000张，问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完．
分析：思考加工一个竖式纸盒需要几张长方形和正方形纸板？加工一个横式纸盒呢？
请填写下表（设加工x只竖式纸盒，y只横式纸盒，恰好能将购进的纸板全部用完）：
根据上表可得方程组$\left\{\begin{array}{l}{x+2y=1000}\\{4x+3y=2000}\end{array}\right.$；解这个方程组，得$\left\{\begin{array}{l}{x=200}\\{y=400}\end{array}\right.$．
（2）该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板50张，长方形纸板a张，全部加工成上述两种纸盒，且120＜a＜136，试求在这一天加工两种纸盒时，a的所有可能值．
（1）若该厂购进正方形纸板1000张，长方形纸板2000张，问竖式纸盒，横式纸盒各加工多少个，恰好能将购进的纸板全部用完．
分析：思考加工一个竖式纸盒需要几张长方形和正方形纸板？加工一个横式纸盒呢？
请填写下表（设加工x只竖式纸盒，y只横式纸盒，恰好能将购进的纸板全部用完）：
| x只竖式纸盒中 | y只横式纸盒中 | 合计 | |
| 正方形纸板的张数 | x | 2y | 1000 |
| 长方形纸板的张数 | 4x | 3y | 2000 |
（2）该工厂某一天使用的材料清单上显示，这天一共使用正方形纸板50张，长方形纸板a张，全部加工成上述两种纸盒，且120＜a＜136，试求在这一天加工两种纸盒时，a的所有可能值．
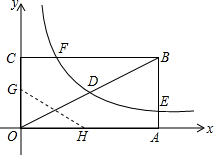如图，矩形OABC的边长OA=8，顶点A、C分别在x、y轴的正半轴上，点D为对角线OB的中点，反比例函数y=$\frac{k}{x}$（k≠0）在第一象限内的图象经过点D、E、F，且tan∠BOA=$\frac{1}{2}$．
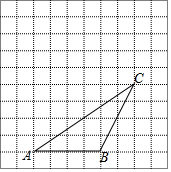如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移2格．
3．
如图，由3个大小完全一样的正方体组成的几何体的主视图是（ ）
如图，由3个大小完全一样的正方体组成的几何体的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
20．下列各组数是三角形的三边，不能组成直角三角形的一组数是（ ）
| A． | 3，4，5 | B． | 6，8，10 | C． | 1.5，2，2.5 | D． | $\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$ |
